四阶偏微分方程

以二维的四阶偏微分方程为例，我们一起来看一下如何使用 FEtch 系统快速地求解偏微分方程问题。

问题描述

定义在区间 $[0,1]\times[0,1]$ 上的函数 $u(x,y)$，满足如下的四阶偏微分方程

\[\frac{\partial^2u}{\partial x^2}-\frac{\partial^4u}{\partial y^4}=f(x,y)=(2-x^2)e^{-y}\]

边界条件为 $u(x,0)=x^2,\ u(1,y)=e^{-y},\\ u(x,1)=x^2/e,\ u(0,y)=0,\\ u_{yy}(x,0)=x^2,\ u_{yy}(x,1)=x^2/e$

已知该问题的理论解为 $u(x,y)=x^2e^{-y}$ 。求函数 $u(x,y)$ 的有限元解。

求解策略

为了简便，我们对方程进行降阶，令 $v=u_{yy}$，那么待求解方程可以写为 $\frac{\partial^2u}{\partial x^2}-\frac{\partial^2v }{\partial y^2}=f(x,y)=(2-x^2)e^{-y}$

\[\frac{\partial^2 u}{\partial y^2}=v\]

此时，边界条件下图所示

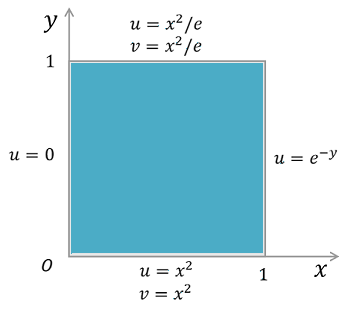
运用变分原理，原方程的弱形式为

$\int_{\Omega}\Big(-\frac{\partial u}{\partial x}\frac{\partial \delta u}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial \delta u}{\partial y}\Big)d \Omega=\int_{\Omega}f \delta ud \Omega$ $\int_{\Omega}\big(\frac{\partial u}{\partial y}\frac{\partial \delta v}{\partial y}+v \delta v\big) d \Omega=0$

脚本文件

这是一个比较简单的单物理场问题。用有限元语言表述，只需要填写 4 种类型的文件，即 PDE、NFE、GCN 和 MDI 文件。

PDE 文件 (uv.pde)，用于描述微分方程的弱形式。在有限元理论框架中，对应于单元矩阵的计算，是整个程序中最核心的部分。

defi
disp u v
coor x y
shap %1 %2
gaus %3
mate ek 1.0

stif
$c6 f=(2-x*x)*dexp(-y)
dist = -[u/x;u/x]+[v/y;u/y]+[u/y;v/y]+[v;v]

load = +[u]*f

end

NFE 文件 (mixa.nfe)，与 PDE 文件相配合，用于给出待求解的矩阵格式的线性方程组（对应于整体矩阵组装），以及对计算结果作进一步处理。

defi
stif s
load f

equation
matrix = [s]
forc = [f]

solution u
gidpost("u v",1.0) u(1),u(2)

end

GCN 文件 (mix.gcn)，用于定义求解器类型。同时与 NFE 文件相配合，一起组织计算流程。

defi
a ell

#startnin a
#solvnin a

MDI 文件 (mix.mdi)，用于组织管理物理场信息。

2dxy
#a 0 2 u v
pde uv q4g2
#

实际操作中，这里的 NFE 文件可以调用系统的库文件自动生成，因此用户只需填写 PDE、GCN 和 MDI 三个文件即可，统计下来，总行数不超过 20 行！

我们通过 FEtch 客户端提交脚本文件后，会自动生成并下载有限元程序文件（mix.exe 和 run.bat）、材料参数文件（mix.mat）和 GiD 软件的前处理模板文件（mix.cnd 和 mix.bas）。编程任务至此已经顺利完成。

前处理

前处理是通过第三方软件 GiD 来完成的。

我们首先进入 GiD 软件界面进行前处理。依次进行几何建模、施加边界条件、赋材料值和网格剖分。特别要注意边界条件的施加，具体效果如下：

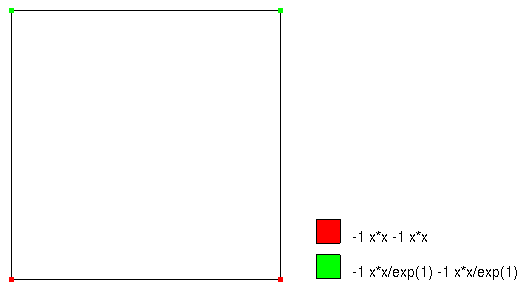
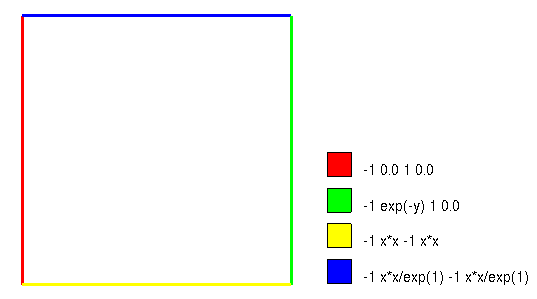
网格划分为 $20\times20$ 个均匀分布的 4 节点线单元。最终导出计算所需的数据输入文件（mix.dat)。

计算结果

经过计算，生成了后处理文件（mix.flavia.res）。将计算结果绘图，并与解析解对比，如下图所示。

有限元解分布图

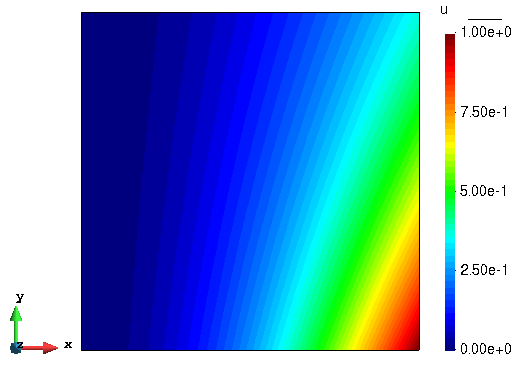
理论解分布图

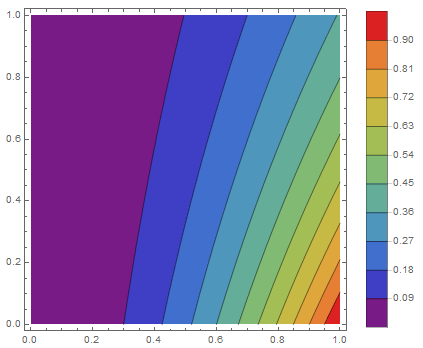
有限元解和理论解的对比图

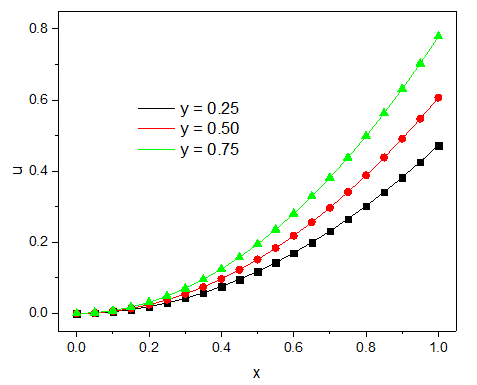
图中的实线为有限元解，散点为理论解。可以看出，两者吻合得很好。至此，四阶偏微分方程的求解已顺利完成。

参考文献

[1] https://www.zhihu.com/question/58781933/answer/2089058091