弹性力学悬臂梁问题
以典型的悬臂梁问题为例,我们一起来看一下如何使用 FEtch 系统快速地求解弹性静力学问题。
问题描述
如图所示,悬臂梁的长度 $L=2\ \rm m$ ,截面高度 $h=10\ \rm cm$ ,宽度 $b=5\ \rm cm$ ,左端约束,右端受集中载荷 $F=10000\ \rm N$ 的作用。弹性模量 $E=200\ \rm GPa$ ,泊松比 $\nu=0.3$ 。试用有限元方法计算该悬臂梁的变形大小。
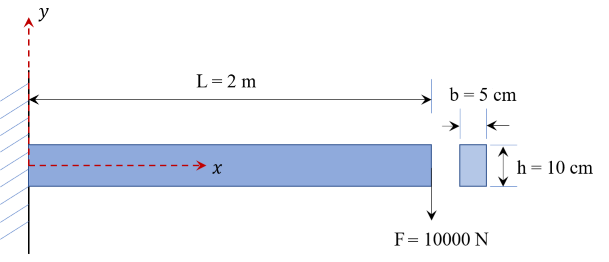
该问题在材料力学中有一个解析解
\[w=\frac{Fx^2}{6EI}(3L-x)\quad\quad\]其中,$w$ 为变形挠度,$I=bh^3/12$ 为截面惯性矩。
控制方程
可以将上述问题看作是弹性力学里的平面应力问题。本构方程是 \(\left\{ \begin{aligned} &\sigma_{xx} \\ &\sigma_{yy} \\ &\sigma_{xy} \end{aligned} \right\}=\frac{E}{1-\nu^2} \begin{gathered} \begin{bmatrix} 1 & \nu &0\\ \nu & 1&0\\0&0&1-\nu\end{bmatrix} \end{gathered}\left\{ \begin{aligned} &\varepsilon_{xx} \\ &\varepsilon_{yy} \\ &\varepsilon_{xy} \end{aligned} \right\}\)
其中 $\boldsymbol{\sigma}$ 表示应力张量, $E$ 为弹性模量, $\nu$ 为泊松比,$\boldsymbol\varepsilon$ 表示应变张量,其定义为
\[\varepsilon_{ij}=\frac{1}{2}(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^T)=\frac{1}{2}\Big(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\Big)\]式中 $\boldsymbol{u}$ 表示位移。本构方程可以写成拉梅方程的形式
\[\sigma_{ij}=\lambda\delta_{ij}\nabla\cdot\boldsymbol{u}+2\mu\varepsilon_{ij}\]其中,拉梅参数 $\lambda=E/(1-\nu^2)$ ,$ \mu={E}/{[2(1+\nu)}]$ , $\delta_{ij}$ 表示克罗内克符号。
弹性体的平衡微分方程为
\[\nabla\cdot \boldsymbol{\sigma}+\boldsymbol{f}=0\ \left(\text{in } \Omega\right)\]边界条件为
\[\boldsymbol{u}=\boldsymbol{u}_0 \ \left(\text{on } \Gamma_1\right)\\ \boldsymbol{T}=\boldsymbol{T}_0 \ \left(\text{on } \Gamma_2\right)\]其中,$\boldsymbol{f}$ 表示体积力,$\boldsymbol{u}_0$ 和 $\boldsymbol{T}_0$ 分别为边界 $\Gamma_1$ 和 $\Gamma_2$ 上指定的位移和外力。
根据弹性体的虚功原理,微分方程的变分形式为 \(\int_\Omega{\boldsymbol{\sigma}:\boldsymbol{\varepsilon(\boldsymbol{\delta u})}}d\Omega=\int_\Omega\boldsymbol{f}\cdot\boldsymbol{\delta u}d\Omega+\int_{\Gamma_2}\boldsymbol{T}\cdot\boldsymbol{\delta u} d\Gamma\)
其中,$\boldsymbol{\delta u}$ 表示虚位移。再将本构方程代入上式,可得
\[\int_\Omega\lambda({\nabla\cdot \boldsymbol{u}})({\nabla\cdot \boldsymbol{\delta u}})+\int_\Omega{2\mu\boldsymbol{\varepsilon}(\boldsymbol{u}):\boldsymbol{\varepsilon}(\boldsymbol{\delta u})}=\int_\Omega{\boldsymbol{f}\cdot\boldsymbol{\delta u}}+\int_{\Gamma_2}\boldsymbol{T}\cdot\boldsymbol{\delta u} d\Gamma\]脚本文件
这是一个比较简单的单物理场问题。用有限元语言表述,只需要填写 5 种类型的文件,即 PDE、FBC、NFE、GCN 和 MDI 文件。
- PDE 文件 (disp.pde),用于描述微分方程的弱形式的体积分项。在有限元理论框架中,对应于单元矩阵的计算,是整个程序中最核心的部分。
defi
disp u v
coor x y
func exx eyy exy
shap %1 %2
gaus %3
mate pe pv fu fv 2.0e11 0.3 0.0 0.0
$c6 fact = pe/(1.+pv)/(1.-pv)
$c6 shear = (1.-pv)/2
func
exx = +[u/x]
eyy = +[v/y]
exy = +[u/y]+[v/x]
stif
dist = +[exx;exx]*fact
+[exx;eyy]*pv*fact
+[eyy;exx]*pv*fact
+[eyy;eyy]*fact
+[exy;exy]*shear*fact
load = +[u]*fu+[v]*fv
end
- FBC 文件 (disp.fbc),用于描述微分方程的弱形式的边界积分项,和 PDE 文件一样用于单元矩阵的计算。
defi
disp u v
coor x
shap %1 %2
gaus %3
mate fu fv -2e6 0.0
stif
null
load = +[u]*fu+[v]*fv
end
- NFE 文件 (elasa.nfe),与 PDE 文件相配合,用于给出待求解的矩阵格式的线性方程组(对应于整体矩阵组装),以及对计算结果作进一步处理。
defi
stif s
load f
equation
matrix = [s]
forc = [f]
solution u
gidpost("u v",1.0) u(1),u(2)
end
- GCN 文件 (elas.gcn),用于定义求解器类型。同时与 NFE 文件相配合,一起组织计算流程。
defi
a ell
#startsin a
#solvsin a
- MDI 文件 (elas.mdi),用于组织和管理物理场的信息。
2dxy
#a 0 2 u v
pde disp q4g2
fbc disp l2g2
#
实际操作中,这里的 NFE 文件可以调用系统的库文件自动生成,因此用户只需填写 PDE、FBC、GCN 和 MDI 四个文件即可,统计下来,总行数不超过 40 行!
我们通过 FEtch 客户端提交脚本文件后,会自动生成并下载有限元程序文件(elas.exe 和 run.bat)、材料参数文件(elas.mat)和 GiD 软件的前处理模板文件(elas.cnd 和 elas.bas)。编程任务至此已经顺利完成。
前处理
首先编辑 elas.mat 文件,定义边界条件的参数。对于当前算例,将悬臂梁右端的切向力转化为均布荷载的形式,大小为 $F/b/h=-10000/0.05/0.1=-2\times10^{-6}\ \mathrm{Pa}$ 。
1 5 aeq4g2
num pe pv fu fv
1 2.0e11 0.3 0 0
#
1 3 all2g2
num fu fv
1 -2e6 0
#
前处理和后处理都是通过第三方软件 GiD 来完成的。
我们首先进入 GiD 软件界面进行前处理。依次进行几何建模、施加边界条件、赋材料值和网格剖分,最终导出计算所需的数据输入文件(elas.dat)。
这里将网格剖分为 $200 \times 10$ 个四边形线性单元。边界条件的施加情况如下
- 左侧位移约束条件

- 右侧均布荷载条件

计算结果
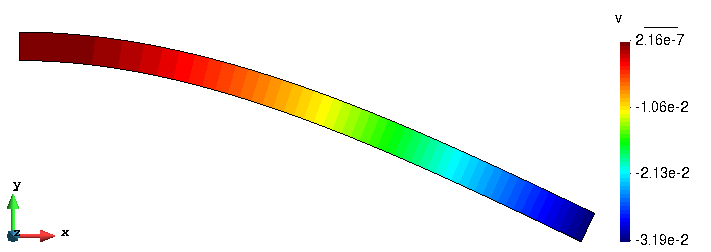
经过计算,生成了后处理文件(elas.flavia.res)。我们再次进入 GiD 软件界面进行后处理,查看云图效果。下图是将变形放大 20 倍后的效果,与预期中的结果一致。
继续取有限元计算得到的中性轴上的竖向变形结果,将其与解析解进行对比,如下图所示。
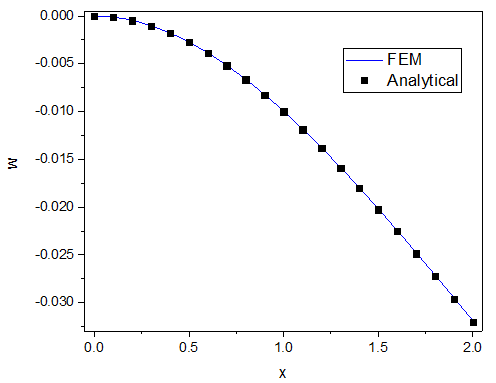
可以看到,有限元解与解析解几乎完全重合,充分证明了算法和程序的可靠性。至此,悬臂梁问题的求解已顺利完成。
参考文献
[1] 徐芝纶. 弹性力学简明教程[M]. 高等教育出版社, 2013.





