Cahn-Hilliard 方程
关键词: 瞬态 非线性 相场 Cahn-Hilliard方程 周期边界
Cahn-Hilliard 方程作为一类重要的 4 阶非线性扩散方程,是相场建模中的经典方程。它最初由 Cahn 和 Hilliard 在 1958 年研究热力学中两种物质之间相互扩散现象时提出,已广泛应用于描述生物种群的竞争和排斥、河床迁移过程、固体表面微粒扩散等物理现象。
本节以二维 Cahn-Hilliard 方程为例,介绍 FEtch 系统在求解相场问题中的应用。
控制方程
微分形式
对于域 $\Omega\subset\mathbb{R}^d\ (1\le d \le 3)$,Cahn-Hilliard 方程为 \(\frac{\partial c}{\partial t}-\nabla \cdot M\left(\nabla\left(\frac{d f}{d c}-\lambda \nabla^{2} c\right)\right)=0 \quad \left(\text{in } \Omega\right) \tag{1}\label{eq1}\)
边界条件为
\[M\left(\nabla\left(\frac{d f}{d c}-\lambda \nabla^{2} c\right)\right)=0 \quad \left(\text{on } \partial \Omega\right) \\ M \lambda \nabla c \cdot n=0 \quad \left(\text{on } \partial \Omega\right) \\\]初始条件为 \(c=c_0 \quad \left(\text{in } \Omega\right)\) 在这里待求变量 $c$ 为序参量(order parameter)。$M$ 和 $\lambda$ 为常数。$f$ 为系统自由能,是序参量 $c$ 的函数。
由于一般的有限元方法只考虑在单元内计算待求变量的一阶导数,上面的四阶微分方程在一般的有限元方法中是没法求解的。为解决这个问题,导入一个新变量,即化学势函数 $\mu=\frac{d f}{d c}-\lambda \nabla^{2} c$ 。这样,方程 (1) 可分解为以下两个二阶微分方程 \(\frac{\partial c}{\partial t}-\nabla \cdot M \nabla \mu=0 \quad \left(\text{in } \Omega\right) \\ \mu-\frac{d f}{d c}+\lambda \nabla^{2} c=0 \quad \left(\text{in } \Omega\right) \tag{2}\label{eq2}\)
弱形式
待求变量为 $c$ 和 $\mu$。根据变分原理,Cahn-Hilliard 方程的弱形式为:求解 $(c,\mu)\in V×V$ 满足
\[\int_{\Omega} \frac{\partial c}{\partial t} \delta c \mathrm{~d} \Omega+\int_{\Omega} M \nabla \mu \cdot \nabla \delta c \mathrm{~d} \Omega=0\ \ \ \forall \delta c \in V \\ \int_{\Omega} \mu \delta \mu \mathrm{~d} \Omega-\int_{\Omega} \frac{d f}{d c} \delta \mu \mathrm{~d} \Omega-\int_{\Omega} \lambda \nabla c \cdot \nabla \delta \mu \mathrm{~d} \Omega=0 \ \ \ \forall \delta \mu \in V \tag{3}\label{eq3}\]算例 1
本算例取自参考文献 [1]。考虑一个二维的 $1\ \mathrm{m}×1\ \mathrm{m} $ 的正方形区域,四周为无流出的自然边界。
初始条件为: $c$ 值随机分布,取 $c_0=0.63+0.02\ (0.5-\mathrm{rand}())$,$\mu$ 值为零。
模型参数为:$M=1$,$f=100\ c^2(1−c)^2$,$\lambda=1×10^{−2}$。
求序参量 $c$ 在 $1\times10^{-3}\ \mathrm{s}$ 内的演化过程。
建模和网格剖分
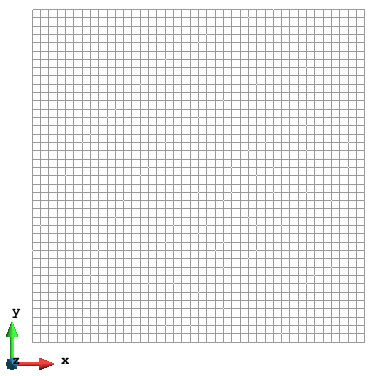
采用通用前后处理软件 GiD 建模,并将网格剖分为 40 × 40 个线性四边形单元。
计算结果
时间步长取 $1\times10^{-6}\ \mathrm{s}$,共 1000 步。对计算结果稍加整理,效果如下。
序参量的演化过程

模拟结束时序参量的分布
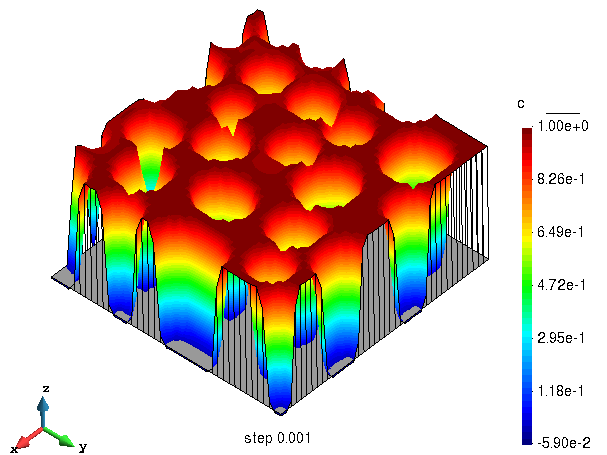
该计算结果可以与参考文献 [1] 和 [2] 比较。由于采用的初始值、网格数和计算方法的不同,计算结果略有差异。
算例 2
本算例取自参考文献 [3] 的 Case Study-XI。考虑一个二维的 $40\ \mathrm{m}×40\ \mathrm{m} $ 的正方形区域,四周为周期性边界条件。
初始条件为: $c$ 值随机分布,取 $c_0=0.4+0.02\ \left(0.5-\mathrm{rand}()\right)$,$\mu$ 值为零。
模型参数为:$M=1$,$f= c^2(1−c)^2$,$\lambda=0.5$。
求序参量 $c$ 在 $100\ \mathrm{s}$ 内的演化过程。
建模和网格剖分
采用通用前后处理软件 GiD 建模,将网格剖分为 40 × 40 个线性四边形单元,并对边界节点施加周期性条件。
计算结果
为节省计算时间,本算例采用自适应时间步长策略。初始时间步长取 $0.02\ \mathrm{s}$,共使用了 467 个时间步。对计算结果稍加整理,效果如下。
序参量的演化过程

模拟结束时序参量的分布
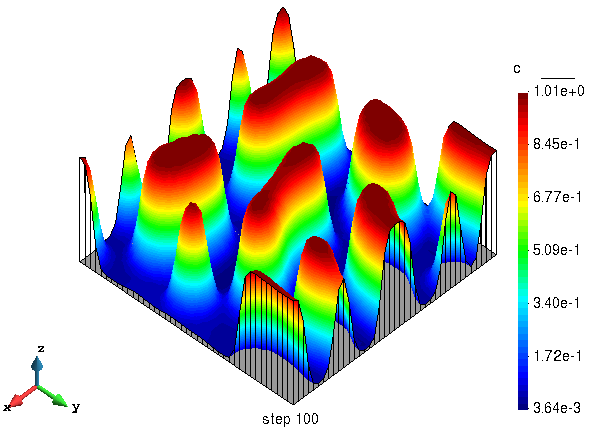
观察发现,计算结果完全满足周期性边界条件的约束。与参考文献 [3] 计算结果进行比较,整体符合得很好,充分证明了算法和程序的有效性。
参考文献
[1] 5. Cahn-Hilliard equation — FEniCS Project
[2] Cahn-Hilliard方程的有限元求解 - 知乎 (zhihu.com)
[3] Biner S B. Programming phase-field modeling[M]. Switzerland: Springer International Publishing, 2017.