天然气水合物开采模拟

天然气水合物是由水和天然气构成的冰状结晶物，因为储量十分丰富，一直被视为潜在的天然气开采资源。然而，由于复杂的赋存环境和固相形态，从天然气水合物中采集天然气是一项非常具有挑战性的工作。较为理想的方法是通过降压、注热和注化学剂等方法，改变储层的环境，打破原有的相平衡条件，使水合物分解，实现对天然气的开采。

本节以一维储层水合物注热开采问题为例，介绍 FEtch 系统在多孔介质多场耦合模拟中的应用。

控制方程

天然气水合物分解方程

天然气水合物在一定的温度和压力条件下会发生分解，其化学反应的具体过程可以表示为： \(\rm{CH_4}·N_h\rm{H_2O} → \rm{CH_4} + N_h\rm{H_2O}\) 即 $1\ \mathrm{mol}$ 的天然气水合物分解后可以生成 $1\ \mathrm{mol}$ 甲烷气体和 $N_h\ \mathrm{mol}$ 的水。式中，$N_h$ 称为水化数，完全水化时 $N_h= 5.75$，对于自然界的水合物，变化范围为 $5.77\sim 7.4$，数值模拟时通常可以取 $6.0$。

孔隙介质中水合物相的质量平衡方程为

式中，$n$ 为孔隙率，$\rho$ 为密度，$S$ 为饱和度，$\dot{m}$ 为质量变化速率。本文中的下标 $h$、$w$ 、$g$ 和 $s$ 分别代表水合物、水、甲烷气体和固体骨架。

根据天然气水合物的分解动力学特征，采用 Kim-Bishnoi 模型，化学反应速率方程可表示为 \({\dot{m}_h}=-{M_h}{K_d}A\langle {P_{eq}}-{P_g}\rangle\)

式中，$P$ 代表压力，$M$ 代表摩尔质量。${K_d}$ 为本征分解速率。$A$ 是单位体积水合物分解的总表面积。$P_{eq}$ 为相平衡压力。

$\langle \rangle$ 为 Macaulay 括弧，当 $\langle x\rangle>0$ 时，$\langle x\rangle=x$；否则，$\langle x\rangle=0$。

相应地，水合物分解的产水和产气速率为 \({\dot{m}_w}=-\left( {M_w}/{M_h} \right){N_h}{\dot{m}_h}\)

气液两相流方程 \(\begin{align} & \left( \frac{n{S_w}}{K_w}-n\frac{\partial {S_w}}{\partial P_c} \right)\frac{\partial {P_w}}{\partial t}+n\frac{\partial {S_w}}{\partial P_c}\frac{\partial {P_g}}{\partial t}-n{S_w}{\beta_w}\frac{\partial T}{\partial t} \\ & +\nabla \cdot {\boldsymbol{w}_w}=\frac{1}{\rho_w}{\dot{m}_w}-\frac{1}{\rho _h}\frac{\partial {S_w}}{\partial {S_h}}{\dot{m}_h} \\ \end{align}\) \(\begin{align} & n\frac{\partial {S_w}}{\partial P_c}\frac{\partial {P_w}}{\partial t}+\left( \frac{n{S_g}}{K_g}-n\frac{\partial {S_w}}{\partial P_c} \right)\frac{\partial {P_g}}{\partial t}-n{S_g}{\beta_g}\frac{\partial T}{\partial t} \\ & +\nabla \cdot {\boldsymbol{w}_g}=\frac{1}{\rho_g}{\dot{m}_g}+\frac{1}{\rho_h}\left(1+\frac{\partial {S_w}}{\partial {S_h}}\right){\dot{m}_h} \\ \end{align}\) 其中，$P_c$ 为毛细压力，$P_c={P_g}-{P_w}$；$\beta$ 为体积热膨胀系数。

Darcy 渗流速度 $\boldsymbol{w}$ 满足 \(\boldsymbol{w}_f=-k{k_f}/{\mu_f}\left( \nabla {P_f}-{\rho_f}\boldsymbol{g} \right), f=w,g\) 式中，$k$ 为孔隙介质的固有渗透率，$k_f$ 为流体的相对渗透率，$\mu_f$ 为流体的粘滞系数，$\boldsymbol{g}$ 为体积力向量。

热传导方程 \(\begin{align} & \varsigma \frac{\partial T}{\partial t}-n{S_w}{\beta_w}T\frac{\partial {P_w}}{\partial t}-n{S_g}{\beta_g}T\frac{\partial {P_g}}{\partial t} \\ & +\left( {\rho _w}{c_w}\boldsymbol{w}_w+{\rho_g}{c_g}\boldsymbol{w}_g \right)\cdot \nabla T-\nabla \cdot \left( \chi \nabla T \right)=\frac{\Delta H}{\dot{m}_h} \\ \end{align}\)

其中，$\varsigma$ 是总热容，$\chi$ 是孔隙介质的热传导系数，$\Delta H$ 是水合物分解过程中的焓变。

总热容 $\varsigma$ 通常表示为 \(\varsigma =\left( 1-n \right){\rho_s}{C_s}+n\left( {S_w}\rho_w{C_w}+{S_g}{\rho_g}{C_g}+{S_h}{\rho_h}{C_h} \right)\)

$C$ 代表某相单位质量的比热容。

基于上述控制方程，我们开发了水合物开采模拟软件 PorousTH2C。该软件采用了全耦合的求解策略，并适当地引入了数值稳定化算法。由于整个软件还在进一步完善中，这里仅展示性地给出部分测试结果。

算例

为了方便测试和分析现有的数值计算软件的准确性，Wilder et al.¹设计了一系列考题，并组织了国际上先进的天然气水合物开采模拟软件的进行计算，包括 Tough+Hydrate²、HydrateResSim³、MH-21 HYDRES⁴、STOMP-HYD⁵和 Houston 大学开发的水合物软件⁶等。这里，我们选择其中的注热开采算例（Problem 3 Case 1）进行模拟。

问题描述

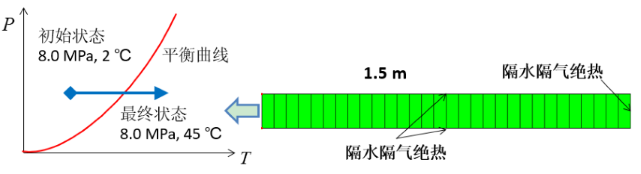
考虑一维的天然气水合物赋存区，长 $L = 1.5\ \mathrm{m}$。开采之前该赋存区完全均匀，各相的饱和度分别为 $S_h = 0.5$，$S_w = 0.5$，$S_g = 0.0$，孔隙水压力和孔隙气压力均为 $8.0\ \mathrm{MPa}$，初始温度为 $2.0\ ^∘\mathrm{C}$。模型参数见下表。

模型的边界条件设定为：

a) 右侧边界，隔气隔水绝热；

b) 左侧边界，$T = 45\ ^∘\mathrm{C}$，$P_w = 8.0\ \mathrm{MPa}$，$P_g = 8.0\ \mathrm{MPa}$；

c) 上下边界均为隔水隔气绝热。

计算结果

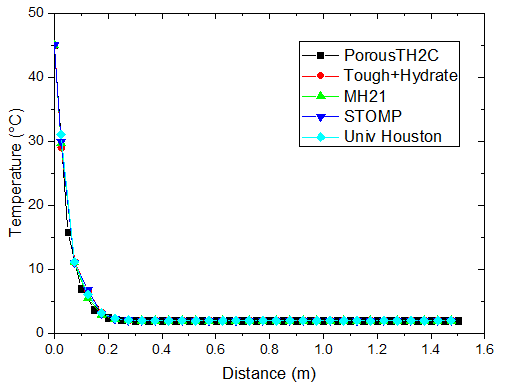
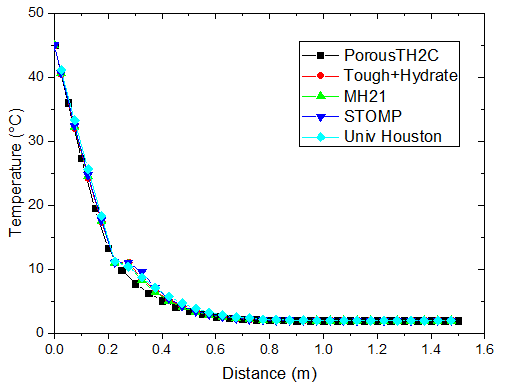
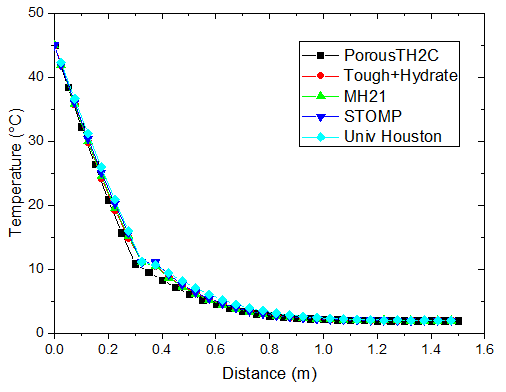
为了符合算例的测试要求，将计算区域剖分成 30 个大小相等的四结点线性等参单元。下图给出了对于注热开采算例的计算结果，展示了不同时刻温度、水合物饱和度、孔隙气压力和甲烷饱和度的分布情况。为了方便对比，图中同时还可给出了其他四种国际先进水平的模拟软件的计算结果。这四款软件包括 Tough+Hydrate²、MH-21 HYDRES³、STOMP-HYD⁵ 和 Houston 大学开发的水合物软件⁶。它们对本算例的模拟结果都可以在美国能源部的网站上找到⁷。

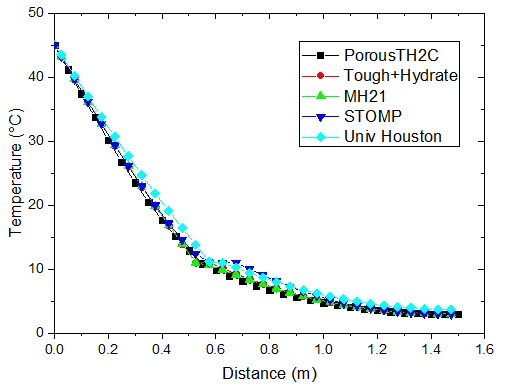
不同时刻温度的分布

t = 1 h	t = 12 h
t = 1 d	t = 3 d

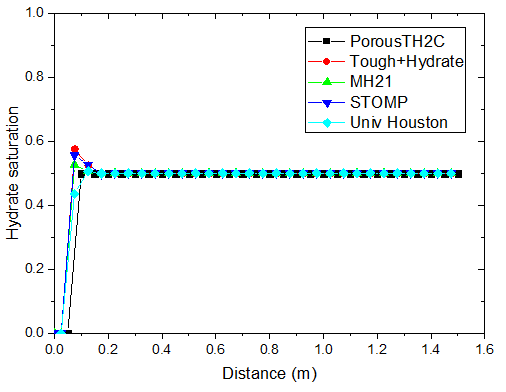
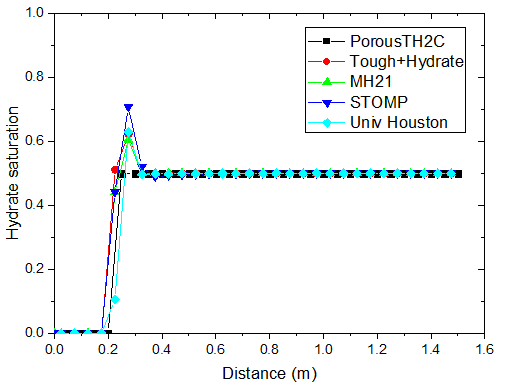
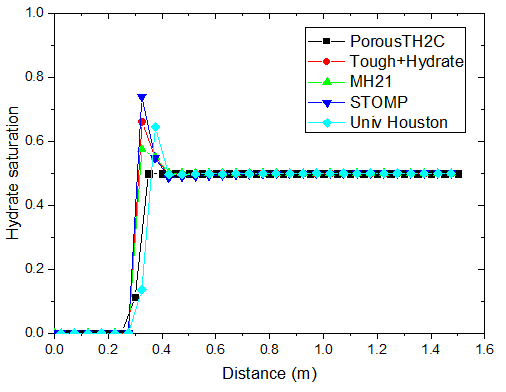
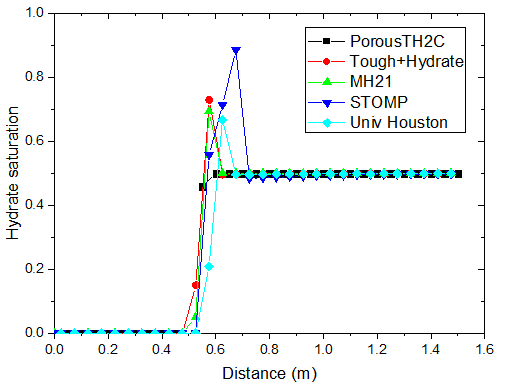
不同时刻水合物饱和度的分布

t = 1 h	t = 12 h
t = 1 d	t = 3 d

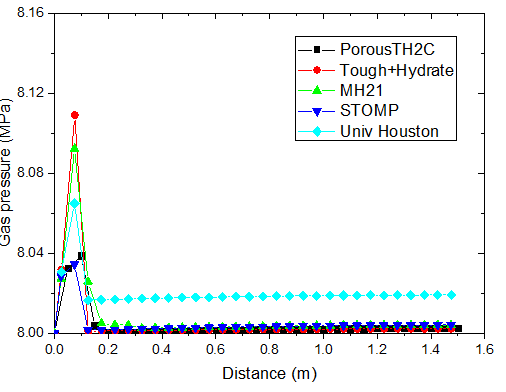
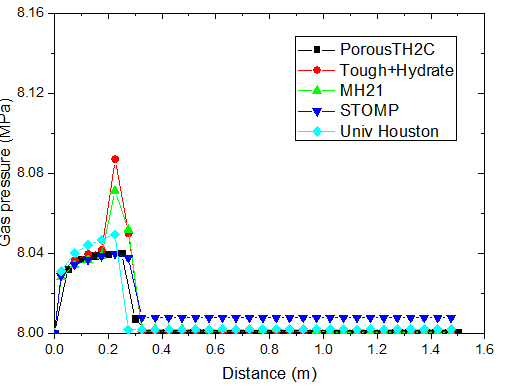
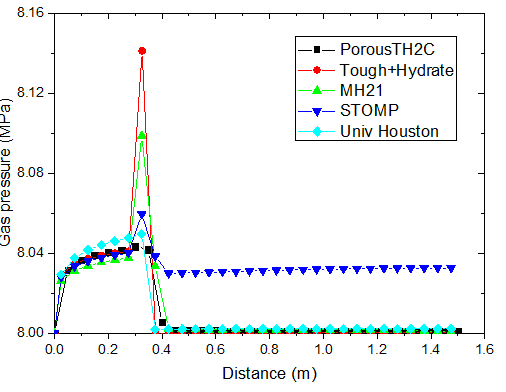
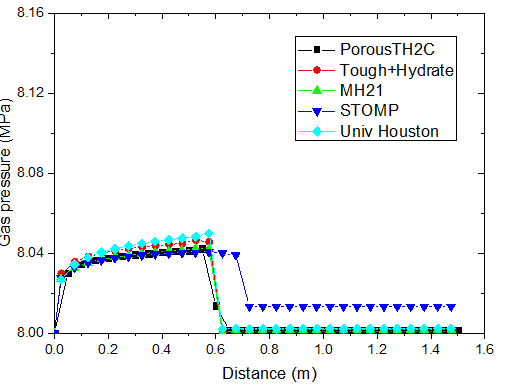
不同时刻孔隙气压力的分布

t = 1 h	t = 12 h
t = 1 d	t = 3 d

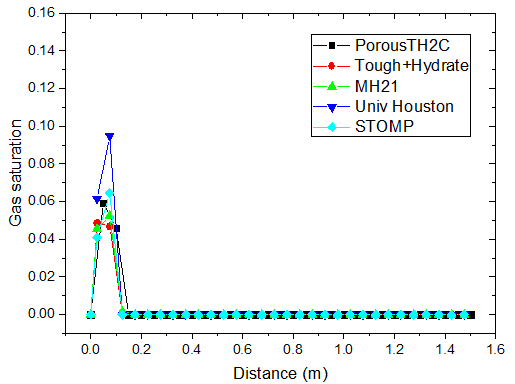
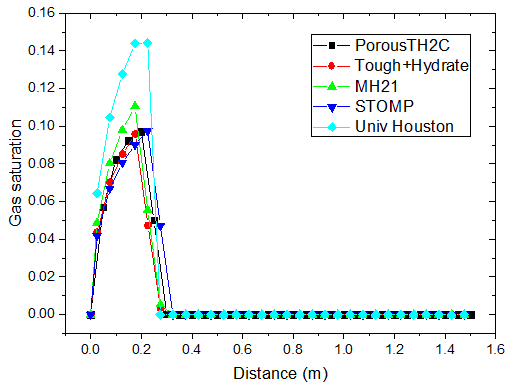
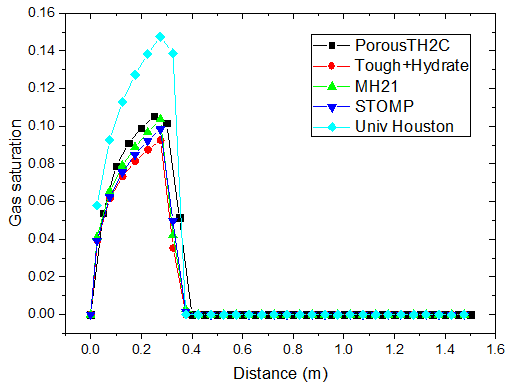
不同时刻甲烷饱和度的分布

t = 1 h	t = 12 h
t = 1 d	t = 3 d

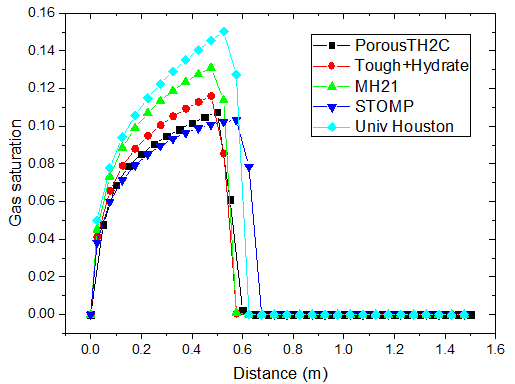对于注热开采模拟，从上图可以看出，随着热传导的进行，储层的温度从左端到右端逐渐升高。升温达到一定水平时，原有的相平衡被打破，导致了水合物的分解，它的含量逐渐降低。水合物分解界面由左向右推进，界面左侧水合物迅速降低为 0。随着水合物的分解，甲烷气体逐渐释放。由于左侧为隔气边界，甲烷气体逐渐积聚，孔隙气压力逐渐升高，含量也稳步上升，部分区域甲烷气体饱和度的峰值超过了 10%。

PorousTH2C 计算得到的结果与其他软件的结果符合得较好。值得注意的是，其他软件在水合物分解前沿出现了数值震荡现象。这种情况并没有在 PorousTH2C 的计算结果中出现，表明了 PorousTH2C 程序在一定程度上具有更好的数值稳定性。

参考文献