多孔介质两相渗流

关键词：瞬态非线性两相渗流毛细作用多孔介质

深入探索多孔介质中的多相流动特征对精准认识地下资源开发利用，例如石油勘探开发、煤层气和页岩气开采、二氧化碳地质封存等领域，具有重要的工程意义。

本节以考虑毛细作用的两相渗流问题为例，介绍 FEtch 系统在多孔介质多相流动计算模拟中的应用。

控制方程

假定孔隙介质中的孔隙均由水和油两种流体完全充满。水相饱和度 $S_w$ 和油相饱和度 $S_o$ 满足: $S_w+S_o=1$ 以孔隙水压力 $P_w$ 和孔隙油压力 $P_o$ 作为基本变量，不考虑流体的压缩性。由孔隙介质中液相和油相的质量守恒方程，可得两相渗流的控制方程为： $\begin{align} & -n\frac{\partial {S_w}}{\partial {P_c}} \frac{\partial {P_w}}{\partial t}+n\frac{\partial {S_w}}{\partial {P_c}}\frac{\partial {P_o}}{\partial t}+\nabla \cdot {w_w}=0 \\ \end{align}$

\[\begin{align} & n\frac{\partial S_w}{\partial P_c}\frac{\partial P_w}{\partial t}-n\frac{\partial {S_w}}{\partial {P_c}} \frac{\partial {P_o}}{\partial t}+\nabla \cdot {w_o}=0 \\ \end{align}\]

式中，$t$ 为时间，$n$ 为孔隙率，${P_c}={P_o}-{P_w}$ 为毛细压力；$\boldsymbol{w}_w$ 和 $\boldsymbol{w}_o$ 是孔隙液体和油体的渗流速度，满足广义的 Darcy 定律，即

\[\boldsymbol{w}_w=-\frac{k k_{rw}}{\mu_w}\left(\nabla P_w-\rho_w \boldsymbol{g} \right)\] \[\boldsymbol{w}_o=-\frac{k k_{ro}}{\mu_o} \left(\nabla {P_o}-\rho_o \boldsymbol{g} \right)\]

其中 $k$ 为孔隙介质的固有渗透率；$\mu_w$、$\mu_o$ 分别为液体和油体的粘滞系数；$\boldsymbol{g}$ 为体积力向量；$k_{rw}$、$k_{ro}$ 分别为液体和油体的相对渗透率，常假设为水相饱和度 $S_w$ 的函数。

毛细压力、相对渗透系数和流体的饱和度相互关联，它们之间的关系通常需要根据试验数据进行拟合。目前已有多种通用模型可以描述，如广泛使用的 Brooks-Corey 模型和 van Genuchten 模型。

Brooks-Corey 模型

\[S_{e}(P_c)=(P_c/P_d) ^{-\lambda} \\ k_{rw}(S_e)= S_e^{2/\lambda+3}\\ k_{ro}(S_e)=(1-S_e^2) (1-S_e^{2/\lambda+1})\]

式中，$P_d$ 和 $\lambda$ 为与多孔介质材料性质相关的模型参数，$S_e=\frac{S_w-S_{wr}}{1-S_{wr}-S_{or}}$ 为有效饱和度，$S_{wr}$ 和 $S_{or}$ 分别为水和油的残余饱和度。

van Genuchten 模型

\[S_{e}(P_c)=\left(1+|\alpha P_c|^n\right)^{-m}\\ k_{rw}(S_e)=\sqrt{S_{e}}\left[1-\left(1-S_{e}^{1 / m}\right)^{m}\right]^{2}\\ k_{ro}(S_e)=\sqrt{(1-S_{e})} (1-S_e^{1/m})^{2m}\]

式中，$\alpha$ 、$n$ 和 $m$ 是与多孔介质材料性质相关的模型参数，通常取 $m=1-1/n$。

算例

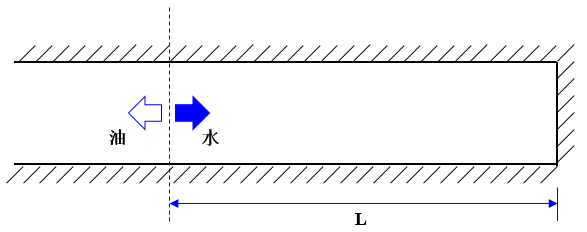
McWhorter 等 [1] 给出了一维两相不相容、不可压缩流体的精确积分解，是两相渗流的经典算例之一。基于该算例，这里考虑一维的水油驱替过程。

模型为长 $L=2\ \mathrm{m}$ 的含油岩芯。一端开口，另一端封闭。从开口端注水，岩芯孔隙中的油在毛细压力的作用下，从开口端流出。不考虑重力作用，求岩芯中水饱和度的演化过程。

初始条件为：筒内的初始水饱和度为 $S_w=0.01$，油压力为 $P_o=0\ \mathrm{Pa}$，对应的水压力为 $P_w=-5\times10^4\ \mathrm{Pa}$。

边界条件为：入口处水的饱和度为 $S_w=1.0$，油压力为 $P_o=0\ \mathrm{Pa}$，对应的水压力为 $P_w=0\ \mathrm{Pa}$。其他位置均为隔水隔油边界。

模型材料使用 Brooks-Corey 模型，具体参数为：

$n=0.3$，$k=10^{-10}\ \mathrm{m^2}$ ，$\mu_w=\mu_o=10^{-3}\ \mathrm{kg/m/s}$，

$P_d=5\times10^3\ \mathrm{Pa}$ ，$\lambda=2$，$S_{wr}=S_{or}=0$。

计算结果

网格剖分采用 2 节点等参线性单元，计算区域被均匀地剖分成了 400 个单元。为了减少计算量，模拟过程中根据迭代收敛速度的快慢动态调整时间步长。共使用了 466 个时间步，2989个迭代步，计算得到了 $10000\ \mathrm{s}$ 内孔隙水饱和度的演化过程。计算结果如下。

孔隙水饱和度的分布

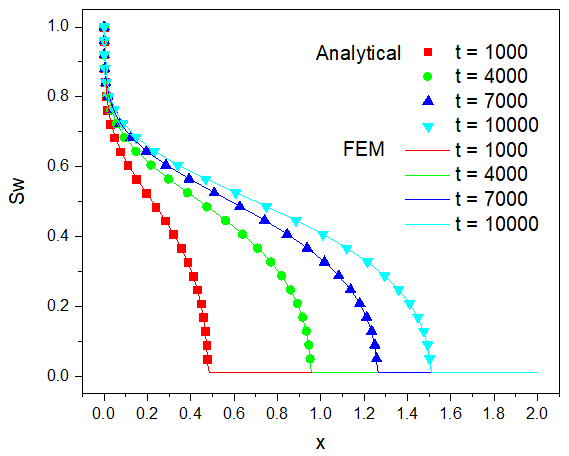
上图给出了不同时刻在水的饱和度的分布图，清晰地展示了驱替过程中油相排出、水相向前推进的过程。

图中的散点为解析解 [2]，实线为计算得到的数值解。对比发现，这里的计算结果与解析解符合得很好，充分证明了算法和程序的有效性。

参考文献

[1] McWhorter D B, Sunada D K. Exact integral solutions for two‐phase flow[J]. Water Resources Research, 1990, 26(3): 399-413.

[2] Fucik R, Mikyska J, Benes M, et al. An improved semi-analytical solution for verification of numerical models of two-phase flow in porous media[J]. Vadose Zone Journal, 2007, 6(1): 93-104.