饱和土体的热固结算例

关键词：瞬态线性饱和土固结流固热耦合全耦合

在热能贮存、地热资源开发、核废料处置、供热管道设计等方面，周围土体在核辐射、地热、季节性温差等产生的高温作用以及冷热循环的作用下，其应力状态和工程性质会发生变化。由此会产生变形、失稳等一系列工程问题。因此，研究温度变化对土体工程性质的影响有着重要意义。

本节以饱和土体的一维热固结问题为例，介绍 FEtch 系统在多孔介质流固热耦合计算模拟中的应用。

控制方程

考虑一个线弹性饱水的非等温的土体，计算简图如下。图中，$q_{0}$ 为瞬时施加的外荷载；$T_0$ 为瞬时施加的温度增量，即超出初始参照温度的增加量；$H$ 为土层厚度。

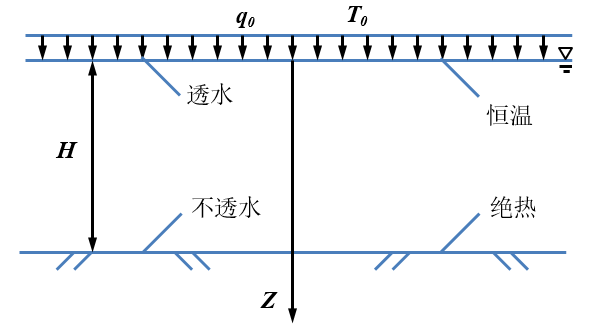
基于动量、质量和能量三个方面的守衡条件，可给出如下的控制方程

力学平衡方程： $(\lambda+2 G) \frac{\partial \varepsilon_{z}}{\partial z}+\frac{\partial p}{\partial z}+\beta \frac{\partial T}{\partial z}=0$ 渗流连续方程： $\frac{\partial \varepsilon_{z}}{\partial t}+\alpha \frac{\partial T}{\partial t}+\frac{k}{\gamma_{w}} \frac{\partial^{2} p}{\partial z^{2}}=0$ 热传导方程： $C \frac{\partial T}{\partial t}=K \frac{\partial^{2} T}{\partial z^{2}}$ 式中，$z$ 为竖向坐标，$t$ 为时间；$\varepsilon_{z}$ 为土体的竖向应变，$\varepsilon_{z}=-\frac{\partial u}{\partial z}$，$u$ 为竖向位移；$p$ 为超静孔隙水压力，简称超静孔压；$T$ 为温度增量，也称为温差，以温度增加为正。

方程中参数的具体含义为：

$\lambda$ 、$G$ 为 $Lame$ 常数（ $G$ 也称为剪切弹性模量），它们与杨氏模量 $E$ 和泊松比 $\mu$ 的关系为

\[\lambda=\frac{E \mu}{(1+\mu)(1-2 \mu)}\] \[G=\frac{E}{2(1+\mu)}\]

$β$ 为热应力系数

\[\beta=(3 \lambda+2 G) \alpha_{s}=\frac{E \alpha_{s}}{1-2 \mu}\]

$\alpha$ 为热膨胀系数

\[\alpha=(1-n) \alpha_s+n \alpha_w\]

其中，$\alpha$、$\alpha_s$、$\alpha_w$ 分别为土体、土颗粒、水的线热膨胀系数，$n$ 为土体的孔隙率。

$k$ 为土体的竖向渗透系数，$\gamma_w$ 为水的重度。
$C$ 为土的体积比热

\[C=(1-n) \rho_{s} C_{s}+n \rho_{w} C_{w}\]

其中，$\rho_s$、$\rho_w$ 分别为土颗粒、水的密度，$C_s$、$C_w$ 分别为土颗粒、水的比热。

$K$ 为土的热传导系数。

该问题是存在解析解的，可参考白冰(2005) [1]的文章。

算例

Aboustit 等(1982) [2] 首次对完全饱和土柱进行了一维热弹性固结分析，是热流固耦合的经典算例之一。该算例取土层厚度 $H=7\ \mathrm{m}$，瞬时施加的外荷载 $q_{0}=1$，温度增量 $T_0=50$。土体的力学、热学和水力基本参数 [3] 如下表所示。

参数	值
$E$	$6\times10^3$
$\mu$	$0.4$
$n$	$0.2$
$k$	$4\times10^{-6}$
$\gamma_w$	$1$
$C$	$167$
$\alpha_s$	$3\times10^{-7}$
$\alpha_w$	$0$
$K$	$0.836$

注：这些参数的量纲并不明确，笔者暂未找到与之匹配的土体类型。这里按无量纲数处理，仅供算例演示使用。

计算结果

以土体竖向位移 $u$、超静孔压 $p$ 和温度 $T$ 为基本变量。网格剖分采用了 2 节点等参线性单元，计算区域被剖分为 50 个单元，并对原点处进行了局部加密。为了减少计算量，模拟过程中使用了变时间步长。初始时间步长取 1 s，并按 1.05 的倍数递增，共使用了 175 个时间步。计算结果如下。

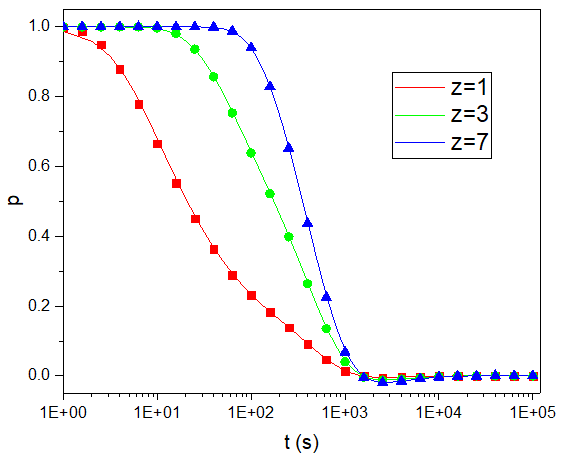
超静孔压随时间的变化

温度随时间的变化

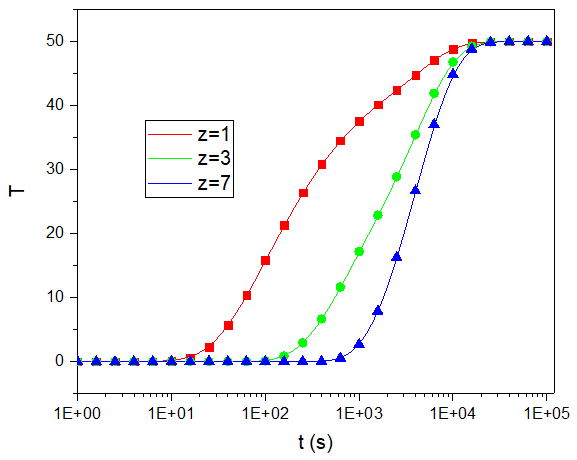
上图给出了土层中不同深度的三个监测点处的超静孔压和温度随时间的演化过程，可以清楚地看到超静孔压逐渐耗散和土体温度逐渐升高的现象。

图中的散点为解析解，实线为计算得到的数值解。对比发现，计算结果与解析解符合得很好。

土层沉降随时间的变化

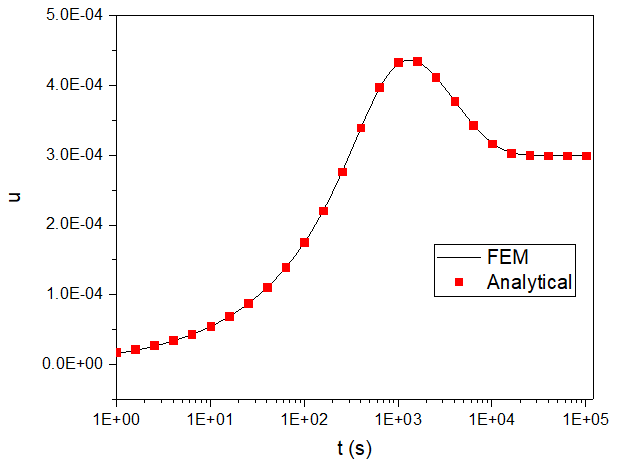
土层沉降是外荷载和温度增量共同作用的结果。前期，排水固结占主导地位，土体表面沉降量逐渐增大。后期，随着土体温度的上升，热膨胀发挥了一定作用，土体沉降逐渐停止，随后发生了明显的回弹现象。

对比发现，这里的计算结果与解析解符合得很好，充分证明了算法和程序的有效性。

参考文献

[1] 白冰. 岩土颗粒介质非等温—维热固结特性研究[J]. 工程力学, 2005, 22(5): 186-191.

[2] Aboustit B L, Advani S H, Lee J K, et al. Finite element evaluations of thermo-elastic consolidation[C]. The 23rd US symposium on rock mechanics (USRMS). OnePetro, 1982.

[3] Noorishad J, Tsang C F. Coupled thermohydroelasticity phenomena in variably saturated fractured porous rocks‐‐formulation and numerical solution[M]. Developments in geotechnical engineering. Elsevier, 1996, 79: 93-134.