泊松-玻尔兹曼方程
关键词: 非线性 Poisson-Boltzmann方程 泰勒展开
非线性泊松-玻尔兹曼方程(Poisson-Boltzmann Equation) 在物理学、生物学和化学等学科中有着广泛的应用。

这个模型最早在一个世纪以前由 Debye 和 Hückel 提出,并且进一步被 Kirkwood 所发展。在过去的二十多年里,对该模型的研究兴趣主要集中在数值计算方面。
数值求解非线性泊松-玻尔兹曼方程的困难主要来自方程的非线性指数项。这需要发展一些迭代技术,而不是直接采用标准的数值方法来离散。作为先导性研究,这里尝试将指数项先进行泰勒展开,再进行有限元离散求解。
下面分别针对正指数和负指数这两种不同情况的概念模型,使用 FEtch 系统求解两个简单的一维算例。
正指数项
含正指数项的非线性泊松方程 \(-\frac{d^2u}{d x^2} =\exp \left(u\right)\)
解析解为 \(u=\ln \left(\frac{1}{2} \text{sech}^2\left(\frac{x}{2}\right)\right)\)
取 [0,1] 的封闭区域,边值为
\[u(0)=-0.693147\\ u(1)=-0.933376\]将指数项泰勒展开,得
\[\exp(u)=1+u+\frac{u^2}{2}+\frac{u^3}{6}+O\left(u^4\right)\]采用有限元方法进行数值求解。取 2 节点线性单元,均匀网格剖分,单元长度为 dx=0.01。
计算结果
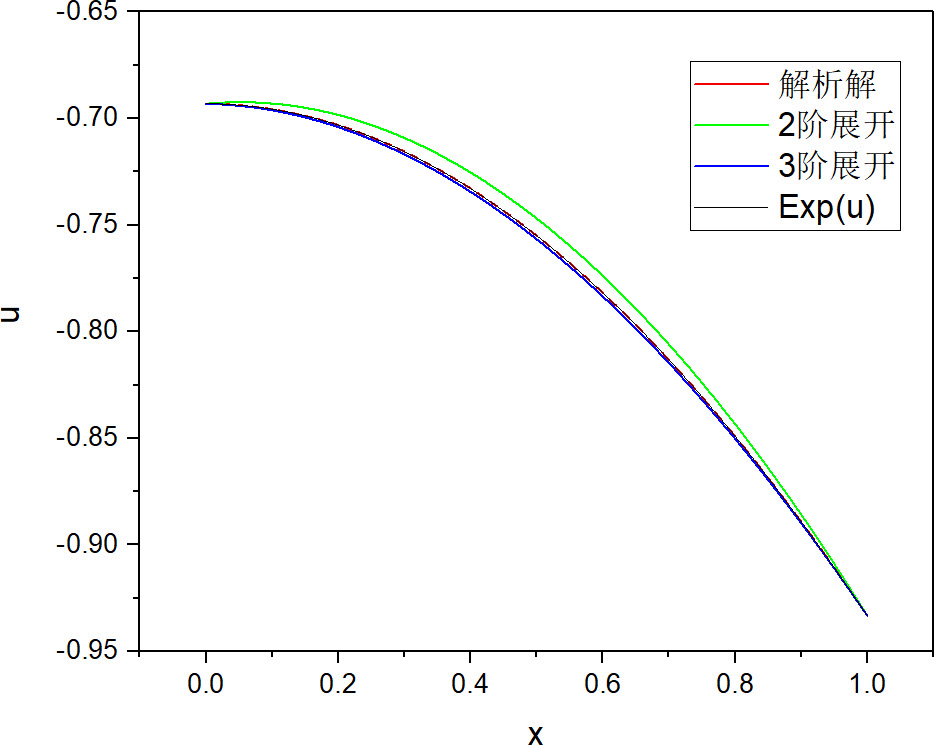
负指数项
含负指数项的非线性泊松方程 \(-\frac{d^2u}{d x^2} =\exp \left(-u\right)\)
解析解为 \(u=\ln \left(2 \sinh ^2\left(\frac{x}{2}\right)\right)\)
取 [0.1,1] 的封闭区域,边值为
\[u(0.1)=-5.29748\\ u(1)=-0.610497\]将指数项泰勒展开,得
\[\exp(-u)=1-u+\frac{u^2}{2}-\frac{u^3}{6}+\frac{u^4}{24}+O\left(u^5\right)\]采用有限元方法进行数值求解。取 2 节点线性单元,均匀网格剖分,单元长度为 dx=0.01。
计算结果
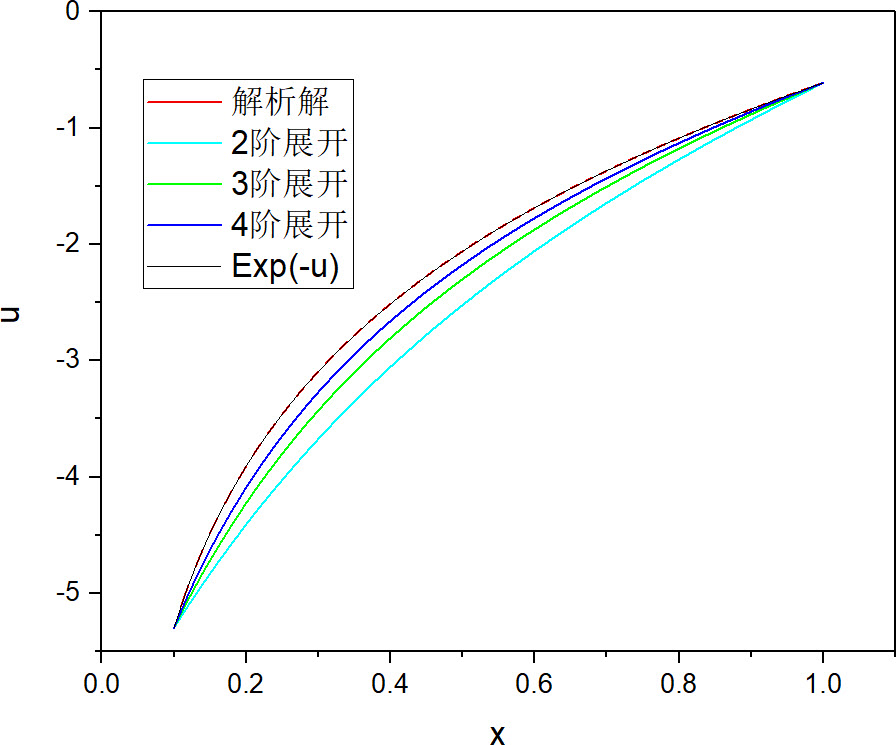
讨论
如果直接针对指数型原函数进行有限元离散,迭代计算对初值会非常敏感,容易出现不收敛的情况。例如,对于含正指数项的算例,当迭代初值为 -50 时,就会求解失败。
如果采用级数展开的方法,则阶次越高计算结果越精确。正指数情况,3 阶展开精度已经基本满足需要。负指数情况,需要 4 阶以上的级数展开。级数展开方法对初值不敏感,收敛性更好。
因此,前期迭代可以考虑采用级数展开方法,计算得到初步的近似值后,继续采用指数型原函数进行迭代,直至计算收敛。