Stefan 问题的解析解算例
关键词: 瞬态 相变 热传导 非线性 向后差分
在自然界和各种工业生产过程中,大量存在着伴有相变的传热过程。例如,冰的融化和凝固,铸造过程中金属铸件的凝固,焊接中焊条的熔化固结,晶体的生长等。其特点是区域内存在着一个随时间移动的两相界面,界面的位置未知,在该界面上放出或吸收潜热。这类问题是1890 年德国科学家 J. Stefan (斯蒂芬) 在研究无限大冰块的融化问题时首先提出的,因而也称为 Stefan Problem (斯蒂芬问题)。
在铸造、焊接、塑料成型等加工工艺中,相变传热是基本的物理现象,与材料性质、产品性能和质量密切相关。研究相变传热的规律及其分析方法,对于设计和改进工艺方法具有重要意义,也是相关工业产品 CAD、CAE 技术的重要基础。
本节以半无限长冰层的融化问题为例,介绍 FEtch 系统在求解伴有相变过程的瞬态热传导问题中的应用。
控制方程
对于二维直角坐标系,固液相变问题服从如下偏微分方程
固相 \(\rho_s c_s \frac{\partial T}{\partial t}-\frac{\partial}{\partial x}\left(k_s \frac{\partial T}{\partial x}\right)-\frac{\partial}{\partial y}\left(k_s \frac{\partial T}{\partial y}\right)=0\ \left(\text{in } \Omega\right) \tag{1a}\) 液相
\[\rho_l c_l \frac{\partial T}{\partial t}-\frac{\partial}{\partial x}\left(k_l \frac{\partial T}{\partial x}\right)-\frac{\partial}{\partial y}\left(k_l \frac{\partial T}{\partial y}\right)=0\ \left(\text{in } \Omega\right) \tag{1b}\]融化界面
\[T=T_f\tag{1c}\] \[k_s\frac{\partial T}{\partial \mathbf{n}_f} \cdot \mathbf{n}_f-k_l\frac{\partial T}{\partial \mathbf{n}_f} \cdot \mathbf{n}_f=\rho_l L\ \frac{d R_f}{dt}\tag{1d}\]其中,$\rho$ 表示材料密度,$c$ 为材料的比热,$T$ 表示温度,$k$ 是热传导系数,下标 $s$、$l$ 分别表示固相和液相。$T_f$ 为凝固/融化温度,$\mathbf{n}_f$ 为相变界面的法向矢量,$L$ 为相变潜热,$R_f$ 为相变界面位置。$x$ 和 $y$ 为二维直角坐标系下的坐标变量,$t$ 为时间。
等效热容法
为了适用于多维问题计算以及处理带有相变区间的情况,这里采用等效热容法。等效热容法不需跟踪两相界面,从而使液相区和固相区统一处理成为可能。此时 (1) 式可统一写成 \(\rho c(T) \frac{\partial T}{\partial t}-\frac{\partial}{\partial x}\left(k(T) \frac{\partial T}{\partial x}\right)-\frac{\partial}{\partial y}\left(k(T) \frac{\partial T}{\partial y}\right)=0\ \left(\text{in } \Omega\right) \tag{2}\) 其中 \(k(T)=\left\{\begin{array}{ll} k_s & \left(T<T_f\right) \\ k_l & \left(T\geqslant T_f\right) \end{array}\right.\)
\[\rho c(T)=\left\{\begin{array}{ll} \rho_s c_s & \left(T<T_f\right) \\ \rho_l L\mathsf{\delta} (T-T_f) & \left(T= T_f\right)\\ \rho_l c_l & \left(T> T_f\right) \end{array}\right.\]式子中的 $\delta(x)$ 为狄拉克 delta 函数。这样我们就将固液相变问题转换成了非线性瞬态热传导问题,可以按照以前讲解过的非线性瞬态问题的求解方法来操作了。
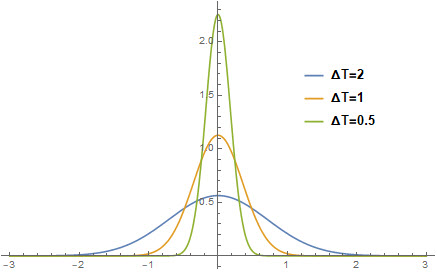
上式的主要难点是 $\delta(x)$ 的数值表示。该函数在除了 $x$ 点以外的点取值都等于零,而其在整个定义域上的积分等于 1。$\delta(x) $ 并不是一个严格意义上的函数,它在泛函分析中被称为广义函数。我们可以用下式来近似表示 delta 函数 \(\delta^*(x)=\frac{\varepsilon}{\sqrt{\pi}} e^{-\varepsilon^2 x^2},\ \varepsilon=\frac{2}{\Delta T}\) 这是一个偶函数,在整个定义域上的积分也等于 1。其中 $\Delta T$ 控制着函数非零区域的宽度,可以理解为假定的以 $x$ 为中心的相变温度区间的一半。 $\Delta T$ 取不同值时对应的曲线形状如下图。
算例
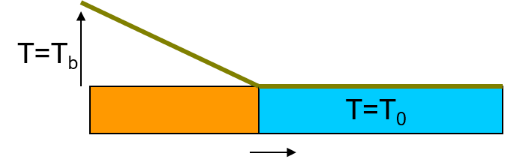
考虑一半无限长的板状冰层,上下边界绝热,初始温度为 $-10 { }^{\circ} \mathrm{C}$。将左端温度提升并保持在 $25 { }^{\circ} \mathrm{C}$,求冰层温度场的演化过程。
有关的热物性参数为:水的比热容 $4.2×10^3 \ \mathrm{J}/\mathrm{kg}/^{\circ}\mathrm{C}$,冰的比热容 $2.1×10^3\ \mathrm{J}/\mathrm{kg}/^{\circ}\mathrm{C}$,水的导热系数 $0.59\ \mathrm{W}/\mathrm{m}/{ }^{\circ}\mathrm{C}$,冰的导热系数 $2.16\ \mathrm{W}/\mathrm{m}/{ }^{\circ}\mathrm{C}$,相变潜热 $333.4×10^3\ \mathrm{J}/\mathrm{kg}$ 。水和冰的密度均取 $1000\ \mathrm{kg}/\mathrm{m}^3$。
建模和网格剖分
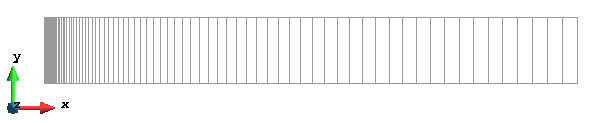
简单起见,这里仅模拟 4 m 长的冰层区域。网格剖分采用 4 节点等参单元,并对左端进行了局部加密。共使用了 80 个单元,162 个节点。
我们令 $\delta^*(x)$ 的参数 $\Delta T=0.5$ ,取 $10^3\ \mathrm{s}$ 为单位时间,对 1200 个时间单位的温度场的演化过程进行模拟。
计算结果
计算程序根据收敛性速度自动改变时间步长,时间步变化范围从 1 到 12,总共使用了 314 个时间步。对计算结果稍加整理,效果如下。
温度场的演化过程

不同时刻的温度场分布
不同时刻的温度场分布情况如下图所示。图中的直线为数值解,散点为解析解。
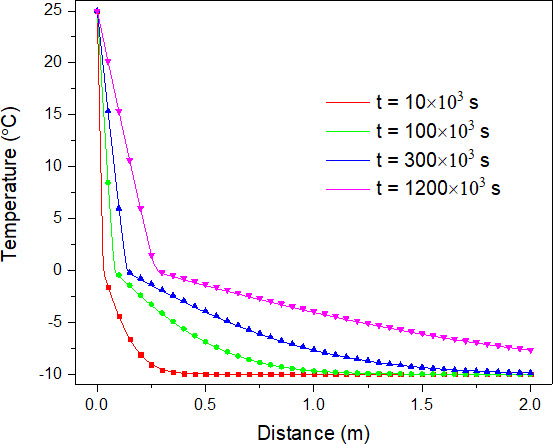
从图中可以看出,随着时间的推移,冰层从左向右逐渐融化,温度不断升高。通过对比可以发现,不同时刻温度场的模拟结果与解析解吻合较好。
温度随时间的变化曲线
选取 0.05、0.1、0.2 和 0.5 m 的四个位置作为观察点,温度随时间变化的过程如下图所示。图中的直线为数值解,散点为解析解。
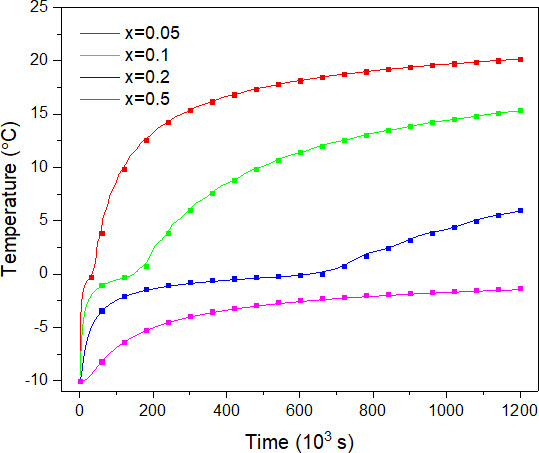
可以看到,伴随着传热过程,观察点由近及远,温度逐渐升高。整个变化过程是平滑和稳定的。数值解和解析解符合较好,充分证明了算法和程序的有效性。