空心圆柱的热应力问题
关键词: 稳态 线性 热弹性 热固耦合 解耦合 平面应变
结构内温度场发生变化时,若受到外部约束或温度场不均匀,就会产生一定的应力,称为热应力。热应力问题的求解在当代工程技术领域中已起到越来越重要的作用。例如,在内燃机、蒸汽轮机 、燃气轮机以及核动力工程等主要设备部件的设计中 ,热应力是必须考虑的问题。
本节以空心圆柱的热应力问题为例,介绍 FEtch 系统在热固耦合计算中的应用。
控制方程
稳态热传导
二维直角坐标系下,稳态热传导服从如下偏微分方程 \(-\frac{\partial}{\partial x}\left(k \frac{\partial T}{\partial x}\right)-\frac{\partial}{\partial y}\left(k \frac{\partial T}{\partial y}\right)=Q \ \left(\text{in } \Omega\right)\) 其中,$T$ 表示温度,$k$ 是热传导系数,$Q$ 为热源密度,$x$ 和 $y$ 为二维直角坐标系下的坐标变量。
这里考虑两类边界条件:
第一类边界条件 \(T=\bar{T} \ \left(\text{on } \Gamma_1\right)\)
第二类边界条件 \(-k\frac{\partial T}{\partial \mathbf{n}} \cdot \mathbf{n}=-q\ \left(\text{on } \Gamma_2\right)\)
其中,$\bar{T}$ 和 $q$ 为边界上的温度和热流值。$\mathbf{n}$ 为边界上的单位外法向量。热流 $q$ 以进入区域为正。
热弹性力学
二维直角坐标系下,忽略惯性力和体力的作用,热弹性力学方程可写成如下形式 \(\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \sigma_{x y}}{\partial y} = 0 \ \left(\text{in } \Omega\right)\)
\[\frac{\partial \sigma_{x y}}{\partial x}+\frac{\partial \sigma_{y y}}{\partial y} = 0 \ \left(\text{in } \Omega\right)\]几何方程为 \(\begin{aligned} \varepsilon_{xx}&=\frac{\partial u}{\partial x}, \\ \varepsilon_{yy}&=\frac{\partial v}{\partial y}, \\ \varepsilon_{x y}&=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \end{aligned}\) 本构方程(平面应变)为 \(\begin{aligned} \left(\begin{array}{c}\sigma_{x x} \\ \sigma_{y y} \\ \sigma_{x y} \end{array}\right)=&\frac{E}{(1+\nu)(1-2\nu)}\left(\begin{array}{ccc} 1-\nu & \nu & 0 \\ \nu & 1-\nu & 0 \\ 0 & 0 & 0.5-\nu \end{array}\right) \left(\begin{array}{l}\varepsilon_{x x} \\ \varepsilon_{y y} \\ \varepsilon_{x y}\end{array}\right) \\ &-\frac{E}{(1-2\nu)}\alpha T\left(\begin{array}{l} 1\\ 1 \\ 0 \end{array}\right) \end{aligned}\) 其中, $u$、$v$ 为位移 $\boldsymbol{u}$ 的分量。 $\varepsilon_{x x}$、$\varepsilon_{y y}$ 、 $\varepsilon_{x y}$ 为应变 $\boldsymbol{\epsilon}$ 的分量,$\sigma_{x x}$ 、$\sigma_{y y}$ 、$\sigma_{x y}$ 为应力 $\boldsymbol{\sigma}$ 的分量。参数 $E$ 为弹性模量,$\nu$ 为泊松比,$\alpha$ 为线膨胀系数。
考虑两类边界条件:
第一类边界条件,给定位移 \(u=u_0,\ v=v_0\ \left(\text{on } \Gamma_1\right)\)
第二类边界条件,给定外力 \(\begin{aligned} T_{x}&=\left(\sigma_{x x},\sigma_{x y}\right)\cdot \mathbf{n}=t_x,\\ T_{y}&=\left(\sigma_{x y},\sigma_{y y}\right)\cdot \mathbf{n}=t_y \quad \left(\text{on } \Gamma_2\right) \end{aligned}\)
其中,$u_0$、$v_0$为边界上的位移;$T_{x}$、$T_{y}$ 分别为边界力在 $x$ 和 $y$ 方向的分量。$\mathbf{n}$ 为边界上的单位外法向量。
算例
无限长的热弹性空心圆柱体,内径为 $R_1=4.5\ \mathrm{m}$,外径为 $R_2=50\ \mathrm{m}$。整个区域初始温度为 $0\ ^∘\mathrm{C}$。外部边界完全约束,保持恒定温度 $T_0=25\ ^∘\mathrm{C}$。内部边界可自由移动。在内部边界上持续进行加热,热源密度为 $q=30\ \mathrm{W}\ \mathrm{m}^{-2}$ 。材料参数为:热传导系数 $k=5.5\ \mathrm{W}\ \mathrm{m}^{-1}\ \mathrm{K}^{-1},$ 弹性模量 $E=2.5\ \mathrm{GPa}$,泊松比 $\nu=0.25$,线膨胀系数 $\alpha=4.2\times10^{-5} /^∘\mathrm{C}$。求圆柱体的温度 $T$ 、径向位移 $u_{r}$ 和径向应力 $\sigma_{r}$ 的分布情况。
这是一个典型的平面应变问题。该问题的解析解为: \(\begin{aligned} u_{r}(r)=&-\frac{q R_{1} \beta}{2 \psi k} r\left(\ln r-\frac{1}{2}\right)+\frac{A_{0}}{2} r+\frac{A_{1}}{r} \\ \sigma_{r}(r)= & \psi\left[-\frac{q R_{1} \beta}{2 \psi k} \left(\ln r+\frac{1}{2}\right)+\frac{A_{0}}{2}-\frac{A_{1}}{r^{2}}\right] \\ & +\lambda\left[-\frac{q R_{1} \beta}{2 \psi k} \left(\ln r-\frac{1}{2}\right)+\frac{A_{0}}{2}+\frac{A_{1}}{r^{2}}\right] \\ & -\beta\left[\frac{R_{1} q}{k} \ln \left(\frac{R_{2}}{r}\right)+T_{0}\right]\\ T(r)=&\frac{R_{1} q}{k} \ln \left(\frac{R_{2}}{r}\right)+T_{0} \end{aligned}\)
其中 $\psi=\lambda+2 G$,$\beta =\alpha \left ( 3\lambda + 2G\right ) $,$\lambda$ 和 $G$ 为 $Lame$ 常数。$A_{0}$ 和 $A_{1}$ 为积分常数。对于当前算例,$A_{0}=5.96 \times 10^{-3}$,$ A_{1}=-1.19 \times 10^{-1}$。
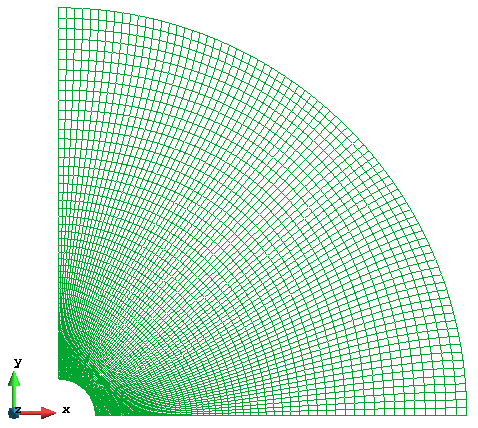
网格剖分
网格剖分采用 4 节点四边形单元。共使用了 6400 个单元,6561 个节点。为了保证计算精度,对内部边界位置的网格进行了局部加密。
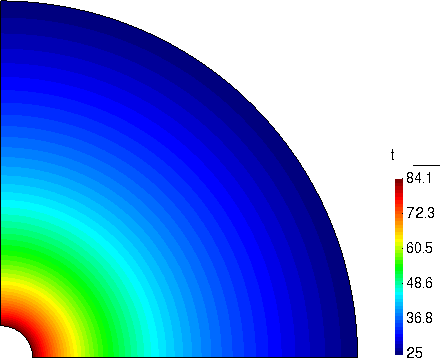
计算结果
温度的分布
位移的分布
水平位移
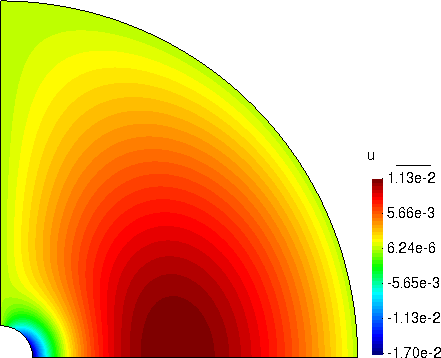
竖向位移
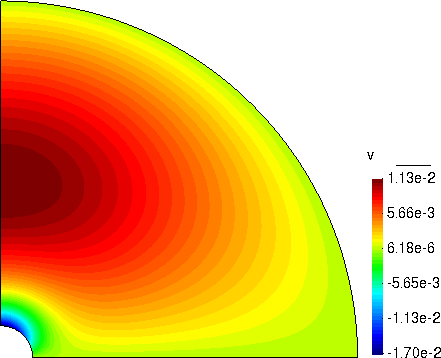
位移模量
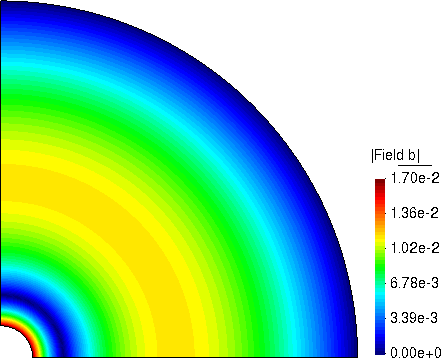
径向位移
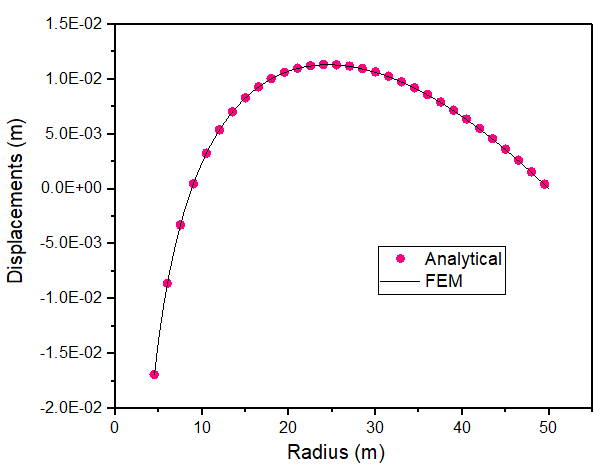
轴向应力的分布
x 方向正应力
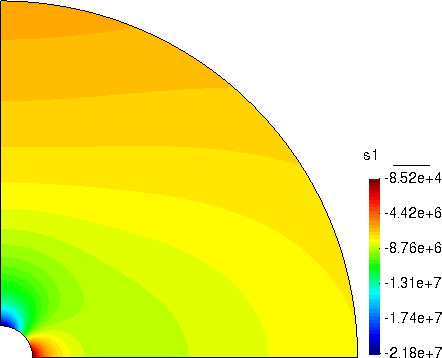
y 方向正应力
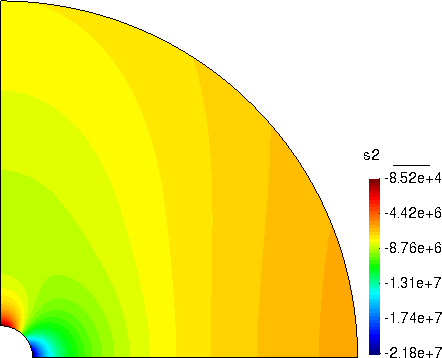
切应力
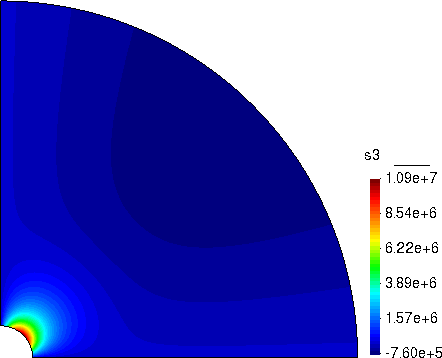
径向应力

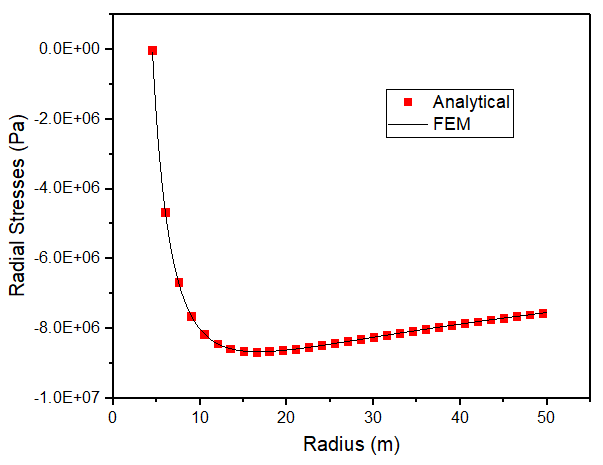
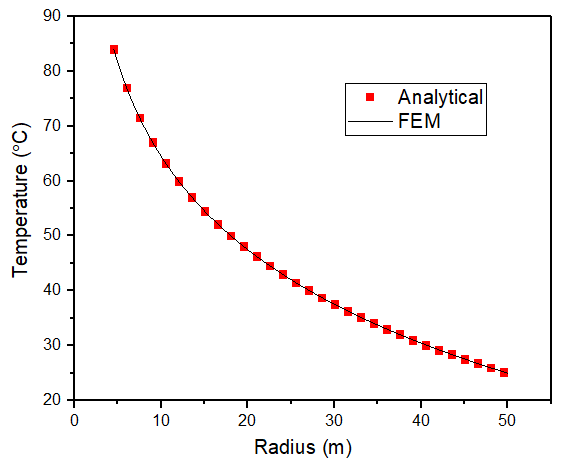
可以看到,数值解和解析解符合较好,充分证明了算法和程序的有效性。
参考文献
[1] 李维特, 黄保海, 毕仲波. 热应力理论分析及应用[M]. 中国电力出版社, 2004.