Biot 动力学方程的解析解算例

关键词：稳态线性土动力学 Biot方程流固耦合

土层动力反应分析是土动力学和地震工程学中重要的研究课题之一。在水工结构、近海岸结构等工程领域有着广泛的应用背景。在土动力学中，饱和土通常被抽象为流固耦合两相介质。M. A. Biot 于 1956 年以固相位移 u 和液相位移 U 为基本未知量建立了两相介质动力问题的控制微分方程，即 u-U 格式的 Biot 动力学方程，奠定了这一领域的研究基础。此后，Zienkiewicz 在此基础上经过一定的简化，推导出了适用于中低频荷载的、以固相位移 u 和孔隙水压力 p 为基本未知量的控制方程，即 u-p 格式。与 u-U 格式的动力学方程相比，混合形式的 u-p 格式动力学方程具有较少的未知量，同时孔压 p 也是大多数土动力学问题中需要求解的关键变量。基于以上原因，u-p 格式的 Biot 动力学方程在土动力学问题的研究中得到了广泛应用，使得求解上述方程的高效数值方法成为土动力学中的重要研究课题之一。

本节以饱和土体的动力固结问题为例，介绍 FEtch 系统在求解 Biot 动力学问题中的应用。

控制方程

对于域 $\Omega\subset\mathbb{R}^d\ (1\le d \le 3)$，动载作用下饱和土体的 Biot 动力学方程为：

\[\frac{\partial^2 \boldsymbol{u}}{\partial t^2}-\nabla\cdot(\boldsymbol{\sigma}-p\boldsymbol{I})=\rho\boldsymbol{f} \ \left(\text{in } \Omega\right) \tag{1a}\label{eq1}\] \[\frac{\partial \epsilon}{\partial t}+\frac{1}{Q}\frac{\partial p}{\partial t}-\nabla\cdot \frac{k}{\gamma_w}\nabla p=\boldsymbol{0} \ \left(\text{in } \Omega\right) \tag{1b}\] \[\boldsymbol{\varepsilon}=\left(\nabla \boldsymbol{u}+\nabla^{T} \boldsymbol{u}\right)/2,\quad\epsilon =\boldsymbol{\varepsilon}:\boldsymbol{I} \tag{1c}\] \[\boldsymbol{\sigma}=\boldsymbol{D} \boldsymbol{\varepsilon} \tag{1d}\]

其中，$\boldsymbol{u}$ 是固相位移，$p$ 是孔隙水压力，$\boldsymbol{\sigma}$ 为有效应力，$\boldsymbol{f}$ 是体力项，$\boldsymbol{\varepsilon}$ 为应变，$\epsilon$ 为体应变。$\nabla$ 为梯度算子，$\boldsymbol{D}$ 为刚度矩阵，$\boldsymbol{I}$ 为单位矩阵。$\rho$ 是土体密度，$k$ 为渗透系数，$\gamma_w$ 为水的容重。$1/Q$ 是表征液体和固体颗粒压缩性的量，依赖于孔隙率 $n$ 和液体与固体颗粒的体积模量 $K_f$ 和 $K_s$

\[\frac{1}{Q}=\frac{n}{K_f}+\frac{1-n}{K_s}\]

算例

考虑 $1\ \mathrm{m}\times 10\ \mathrm{m}$ 的土柱，其弹性模量 $E=20.1\ \mathrm{MPa}$，泊松比 $\nu=0.2$ ，渗透系数 $k=10^{-2}\ \mathrm{m/s}$，水的容重 $\gamma_w = 10^4\ \mathrm{N/m^3}$，孔隙率 $n = 0.33$。孔隙水与固体颗粒的体积模量分别取 $K_f=1.0\times10^7\ \mathrm{MPa}$ 和 $K_s=1.0\times10^9\ \mathrm{MPa}$。初始位移和孔压均为 0 。

边界条件为：底边为固定且不透水边界；上表面为自由透水边界，即孔压为零；左右边界只有竖向位移且不发生横向渗流。

在顶部分别施加以下两种动态荷载，

突加荷载 $f(t)=3.0\ H(t) $
循环荷载 $f(t)=3.0\ \left (1-\cos(75t)\right)$

其中，$H(t)$ 为单位阶跃函数。忽略重力影响，求土柱位移和孔压的变化情况。

网格剖分

模拟过程采用四边形线性等参单元，时间步长取 $10^{-3}\ \mathrm{s}$。网格划分为 160 个单元，205 个结点，在顶端进行了网格局部加密。

计算结果

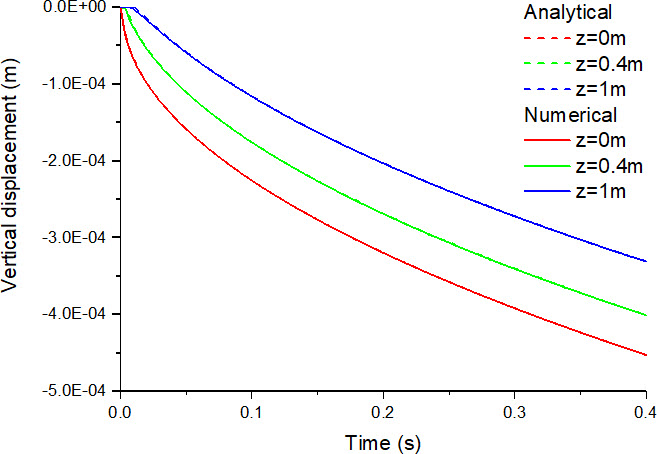
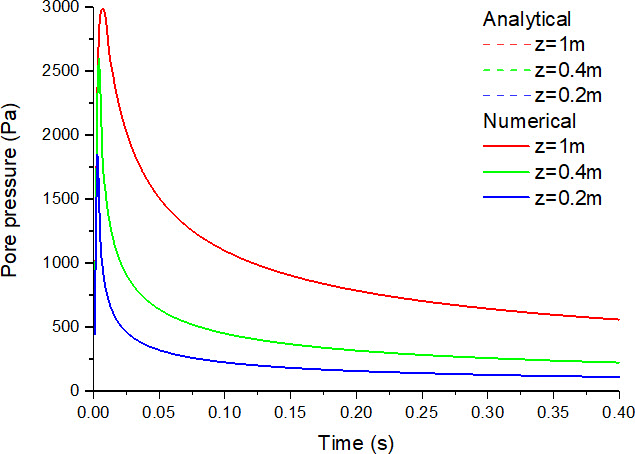
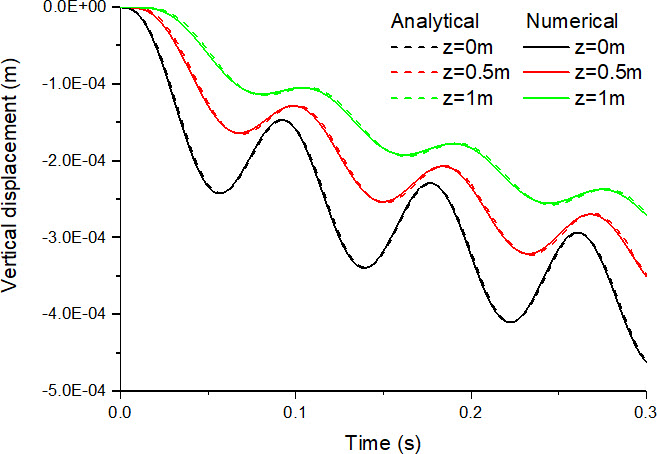
土柱不同深度处的计算结果如下图所示，并与 de Boer（1993）提出的解析解进行了对比。

突加荷载产生的竖向位移

突加荷载产生的孔压

循环荷载产生的竖向位移

循环荷载产生的孔压

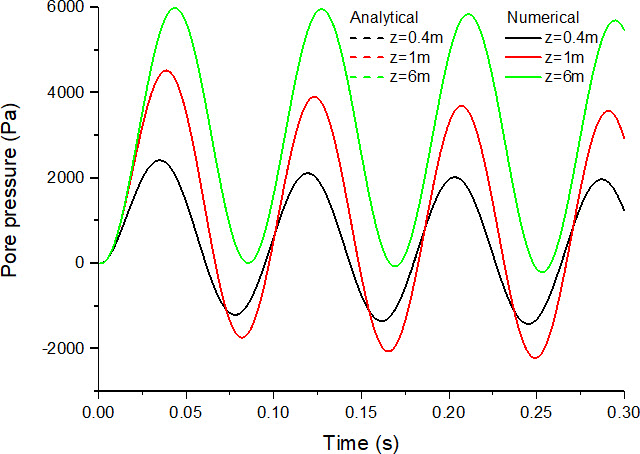
通过与 de Boer 提出的解析解进行对比，可以发现数值解与解析解的结果符合得很好，充分证明了算法和程序的有效性。

参考文献

De Boer R, Ehlers W, Liu Z. One-dimensional transient wave propagation in fluid-saturated incompressible porous media[J]. Archive of applied mechanics, 1993, 63(1): 59-72.