Stokes 方程的解析解算例
关键词: 稳态 线性 Stokes方程 Taylor-Hood单元 点单元
Stokes 流问题是非常重要的流体力学问题,也是流体力学研究的基础。
本节以二维 Stokes 问题和 q9-q4 四边形单元为例,讲解 FEtch 系统在计算流体力学领域的应用。
控制方程
Stokes 方程描述了稳定的不可压缩的低雷诺数流体。 对于域 $\Omega\subset\mathbb{R}^d\ (1\le d \le 3)$,Stokes 方程为:
\[-\mu\Delta \boldsymbol{u} + \nabla p = \boldsymbol{f} \quad \left(\text{ in } \Omega\right) \tag{1a}\label{eq1}\] \[\nabla \cdot \boldsymbol{u} = 0 \qquad \left(\text{ in } \Omega\right) \tag{1b}\]其中,$\boldsymbol{u}:\Omega \to \mathbb{R}^d$ 是速度场,$p:\Omega \to \mathbb{R}$ 是压力场,$\boldsymbol{f}:\Omega \to \mathbb{R}^d$ 是源项, $\mu$ 是黏性系数。
算例
考虑一个二维的 $1\ \mathrm{m}×1\ \mathrm{m}$ 的充满流体的方腔。流体运动满足 Stokes 方程。设黏性系数 $\mu =1.0\ \mathrm{Pa\cdot s}$。给定的解析解为 \(\begin{array}{l} \boldsymbol{u}=\left[\begin{array}{c} \cos (2 \pi y) \sin (2 \pi x) \\ -\cos (2 \pi x) \sin (2 \pi y) \end{array}\right] \end{array}\)
\[p=x^{2}+y^{2}\]由此得到 \(\boldsymbol{f}=\left[\begin{array}{l} 2 x+8 \pi^{2} \cos (2 \pi y) \sin (2 \pi x) \\ 2 y-8 \pi^{2} \cos (2 \pi x) \sin (2 \pi y) \end{array}\right]\)
根据 $\boldsymbol{f}$ 和与解析解相对应的边界条件,求方腔内部的流场速度和压力分布情况。
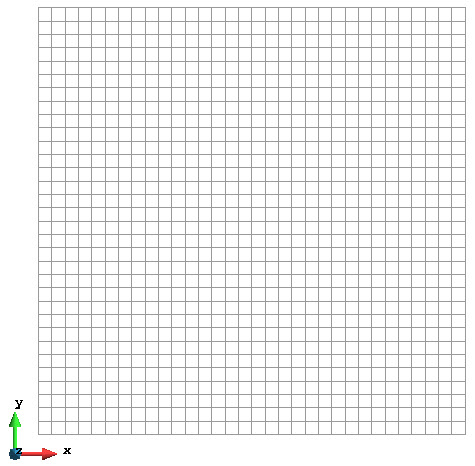
网格剖分
网格剖分采用 9 节点四边形单元。共使用了 1024 个单元,4225 个节点。我们使用了点单元来施加与解析解相对应的边界条件。
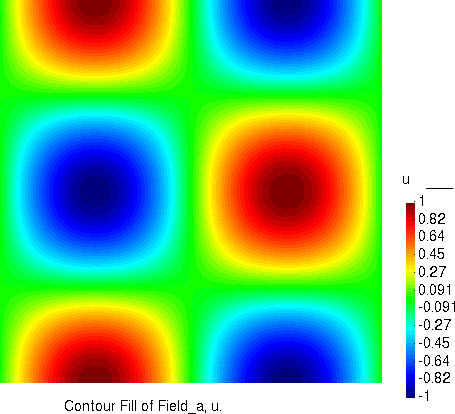
计算结果
水平流速分量的分布
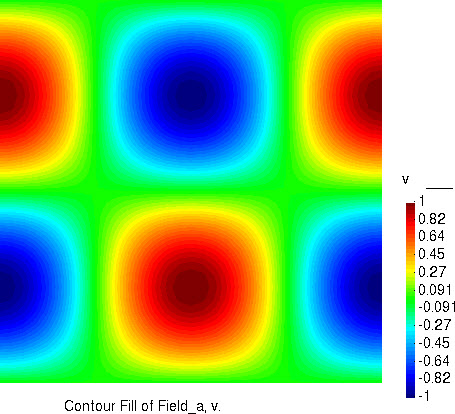
竖直流速分量的分布
流速大小的分布
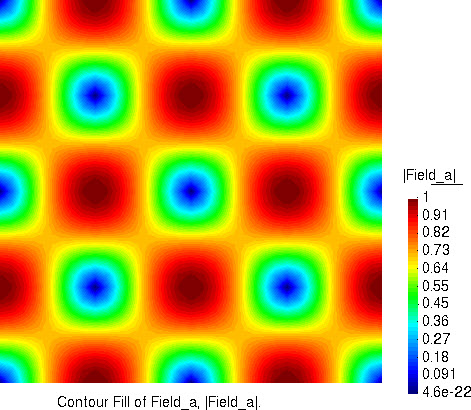
压力的分布
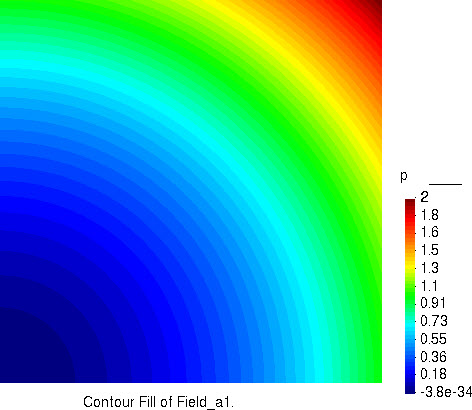
如果继续加密网格进行计算分析,可以进一步提高计算精度,逼近真解,从而验证 Taylor-Hood 单元和计算程序的有效性。这里不再给出具体过程,留给用户自行测试。