非饱和土气液固耦合

关键词：瞬态非线性气液固耦合非饱和土

不管自然界中还是人工制造的孔隙介质，大多都含有可变形的固体骨架。骨架间的连通孔隙中填充着多种不相容的流体，如水、油、空气或者天然气等。在一定的外界扰动下，孔隙介质会发生相互作用的流体渗流过程和骨架变形过程。例如，在渗流过程中，流体压力的变化会影响固体骨架的有效应力，导致固体骨架变形，进而改变孔隙率、固有渗透系数等多种物理性质；反之，固体骨架变形引起的材料性质的变化也会改变流体的速度分布，影响渗流过程本身。因此，在分析孔隙介质的渗流和力学行为时，必须恰当地处理流体流动和固体骨架变形之间的相互作用，即流固耦合作用。

本节以非饱和土体的气液固耦合问题为例，介绍 FEtch 系统在多孔介质流固耦合模拟中的应用。

控制方程

根据渗流力学符号规定的传统，孔隙水压力 ${P_w}$ 和孔隙气压力 ${P_g}$ 均以压为正。毛细压力 ${P_c}={P_g}-{P_w}$。

由孔隙介质中液相和气相的质量守恒方程，可得两相渗流的控制方程为：

\[{S_w}\frac{\partial \nabla \cdot \boldsymbol{u}}{\partial t}+\left(\frac{n{S_w}}{K_w}-n\frac{\partial {S_w}}{\partial {P_c}} \right)\frac{\partial {P_w}}{\partial t}+n\frac{\partial {S_w}}{\partial {P_c}}\frac{\partial {P_g}}{\partial t}+\nabla \cdot \boldsymbol{w}_w=0\] \[\left( 1-{S_w} \right)\frac{\partial \nabla \cdot\boldsymbol{u}}{\partial t}+\left(\frac{n\left( 1-{S_w} \right)}{K_g}-n\frac{\partial {S_w}}{\partial{P_c}} \right)\frac{\partial {P_g}}{\partial t}+n\frac{\partial {S_w}}{\partial {P_c}}\frac{\partial {P_w}}{\partial t}+\nabla \cdot \boldsymbol{w}_g=0\]

式中，$n$ 为孔隙率， $\boldsymbol{u}$ 为固体骨架位移。小变形条件下 $n\approx{n_0}+\left( \alpha -{n_0} \right)\nabla \cdot \boldsymbol{u}$，${n_0}$ 为初始孔隙率，$\alpha$ 为 Biot 系数。$S_w$ 为液体的饱和度，${K_w}$、${K_g}$ 分别为液体和气体的压缩模量，通常 ${K_g}$ 受压力影响较大，可表示为 ${P_g}$ 的函数；$\boldsymbol{w}_w$ 和 $\boldsymbol{w}_g$ 是孔隙液体和气体的 Darcy 流速，满足广义的 Darcy 定律，即

\[\boldsymbol{w}_w=-\frac{k k_{rw}}{\mu_w}\left(\nabla P_w-\rho_w \boldsymbol{g} \right)\] \[\boldsymbol{w}_g=-\frac{k k_{rg}}{\mu_g} \left(\nabla {P_g}-\rho_g \boldsymbol{g} \right)\]

其中 $k$ 为孔隙介质的固有渗透率；$\mu_w$、$\mu_g$ 分别为液体和气体的粘滞系数；$\boldsymbol{g}$ 为体积力向量；$k_{rw}$、$k_{rg}$ 分别为液体和气体的相对渗透率，常假设为液相饱和度 $S_w$ 的函数；$\rho_w$ 和 $\rho_g$ 分别为液体和气体的密度。

在准静态条件下，忽略各相加速度的影响，孔隙介质整体的动量平衡方程为

\[\nabla \cdot \boldsymbol{\sigma} +\rho \boldsymbol{g}=0\]

其中 $\boldsymbol{\sigma} $ 是总应力（以拉为正），$\rho$ 是孔隙介质的总密度。

考虑到岩土材料的非线性特征和有效应力原理，常常采用以下增量形式的应力应变关系式

\[d\boldsymbol{\sigma} =\boldsymbol{D_T}:d\boldsymbol{\varepsilon} -\alpha ({S_w}d{P_w}+{S_g}d{P_g})\boldsymbol{I}\]

式中，$\boldsymbol{\varepsilon}$ 是应变张量，$\boldsymbol{I}$ 是二阶单位张量，$\boldsymbol{D_T}$ 为土体的切线弹性模量矩阵。小变形条件下，应变和位移之间满足 $\boldsymbol{\varepsilon} =\left( \nabla u+\nabla ^T u \right)/2$。

由以上两式，可得

\[\nabla \cdot \left\{ {D_T}:\left( \frac{\partial\boldsymbol{\varepsilon} }{\partial t} \right)-\alpha \left({S_w}\frac{\partial {P_w}}{\partial t}+\left( 1-{S_w}\right)\frac{\partial {P_g}}{\partial t} \right)\boldsymbol{I}\right\}+\frac{\partial \rho }{\partial t}\boldsymbol{g}=0\]

算例

砂柱排水试验

Liakopoulos 砂柱排水试验作为经典算例，经常被用来验证固液气全耦合模型的正确性和计算程序的可靠性。如下图所示，该试验采用高为 $1.00\ \mathrm{m}$、直径为 $0.10\ \mathrm{m}$ 的 Del Monte 砂柱，砂柱底部设透水石，侧面采用圆筒隔水。

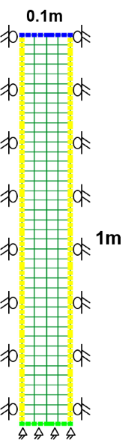
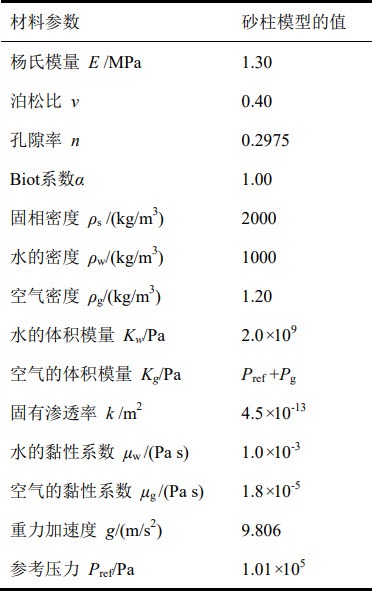
试验开始之前，首先从砂柱顶端注入稳态水流，直至砂柱底端自由排水为止，以确保整个砂柱处于完全饱水状态。试验开始时，试样顶端停止供水。此后，受重力作用，砂柱中的孔隙水逐渐从试样底端排出，砂柱同时发生沉降变形。试验过程中，对砂柱中的水压分布、试样底端的瞬时排水速率和累积排水量进行了记录。假定固体骨架是线弹性材料。砂柱模型的材料参数见下表。

LiakopoulosMat

Del Monte 砂的持水特征曲线和相对渗透系数可以表示为

\[S_w=1-1.9722\times {10^{-11}}\] \[k_{rw}=1-2.207(1-S_w)^{1.0121}\] \[k_{rg}={\left( 1-\frac{S_w-0.2}{0.8} \right)}^2\left [ 1-{\left( \frac{S_w-0.2}{0.8} \right)}^{5/3}\right]\]

其中毛细压力 ${P_c}={P_g}-{P_w}$，单位为 $\mathrm{Pa}$，要求 $S_w>0.91$。

计算结果

合理的选择基本变量是成功模拟多相孔隙介质中非线性全耦合问题的关键一步，这里以固体骨架位移 $\boldsymbol{u}$、孔隙液体压力 $P_w$ 和孔隙气体压力 $P_g$ 为基本变量。网格剖分采用 8 节点等参单元四边形单元，计算区域被结构化地剖分为 160 个单元和 569 个节点。模拟过程中时间步长取 5 s。计算结果如下。

孔隙水压力随时间的变化

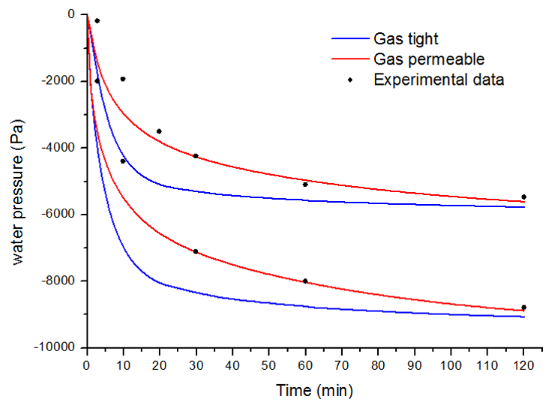
上图给出了砂柱中不同高度的两个监测点处孔隙水压力随时间的演化过程，并对比了砂柱两侧透气和不通气两种边界条件下的计算结果。可以看出，假定两侧为透气条件时计算结果与试验实测结果吻合较好，也说明了气液固三相模型可以很好地模拟自由排水条件下的非饱和渗流过程。

孔隙水饱和度的分布

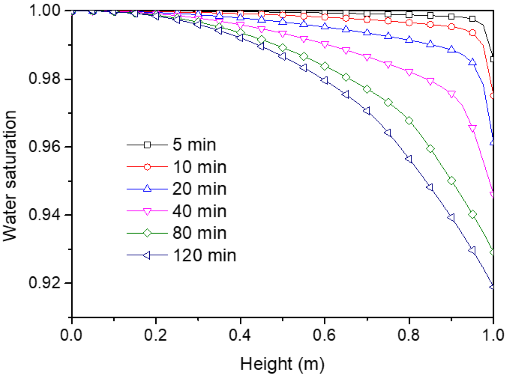
上图给出了不同时刻在砂柱中心线处水体饱和度的纵向分布图，清晰地展示了排水过程中水位线向下推进的过程。

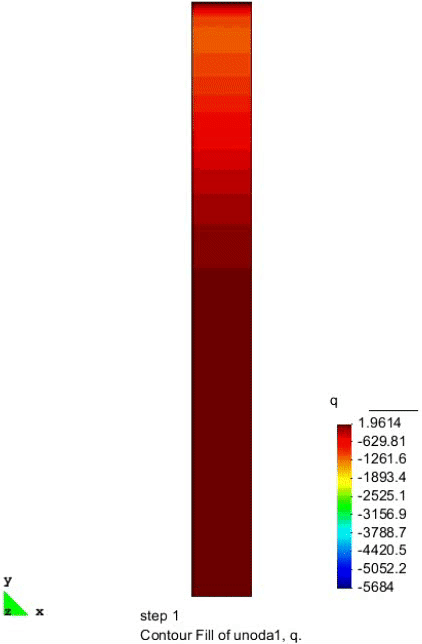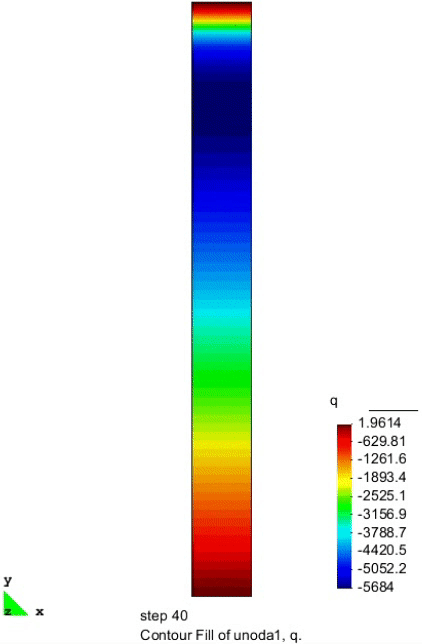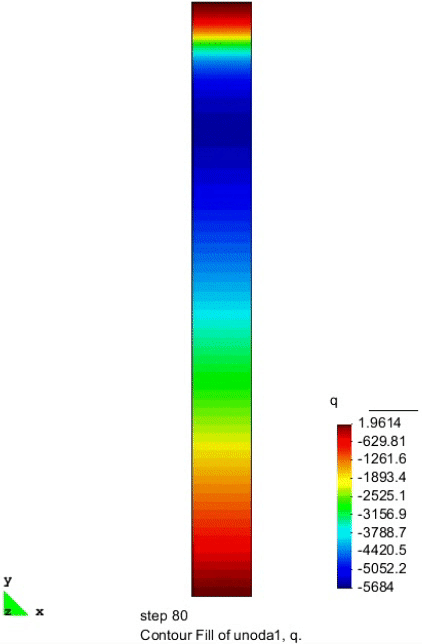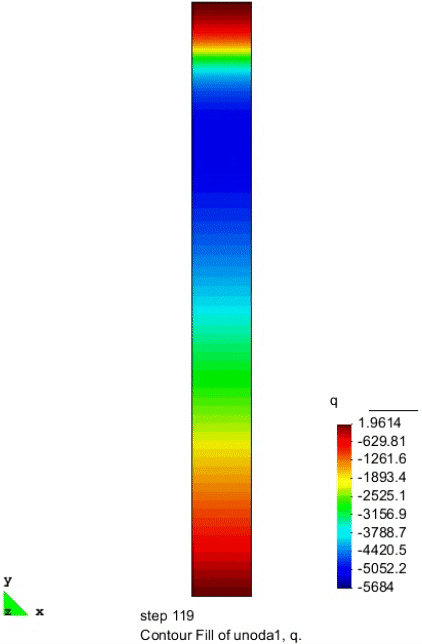
孔隙气压力的分布

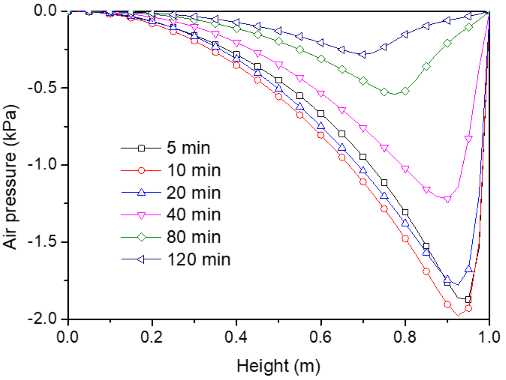
上图给出了不同时刻在砂柱中心线处孔隙气压力的纵向分布图。随着水从砂柱中排出，非饱和区域首先在砂柱顶部形成，并存在一定的真空，有较低的负气压出现。负气压区域逐渐向砂柱中部移动。随着外部气体的进入，负孔压值逐渐趋于 0。

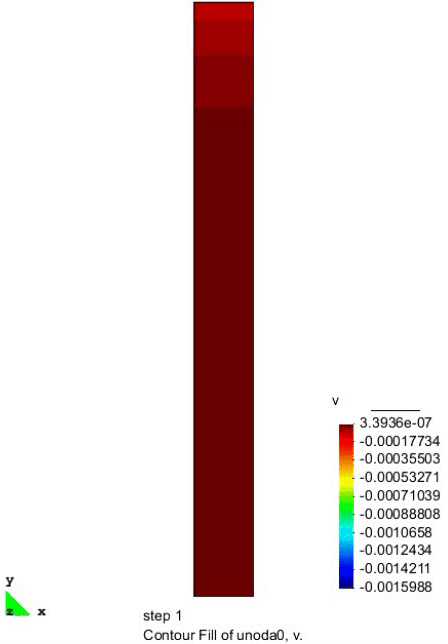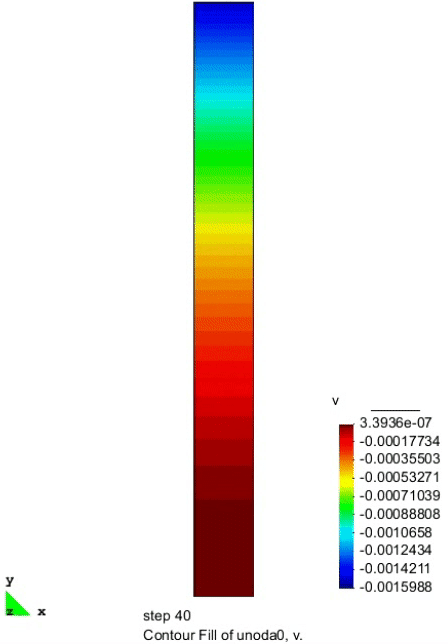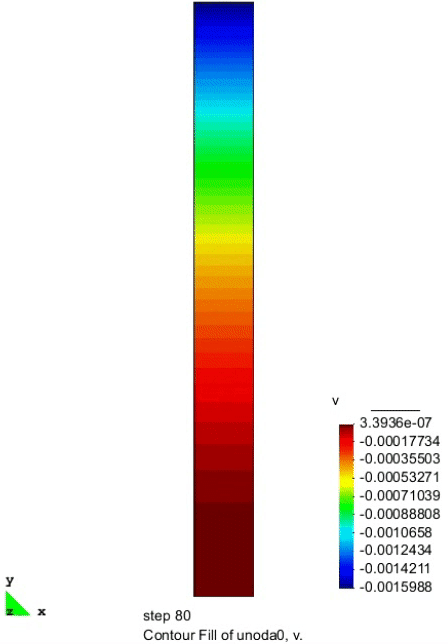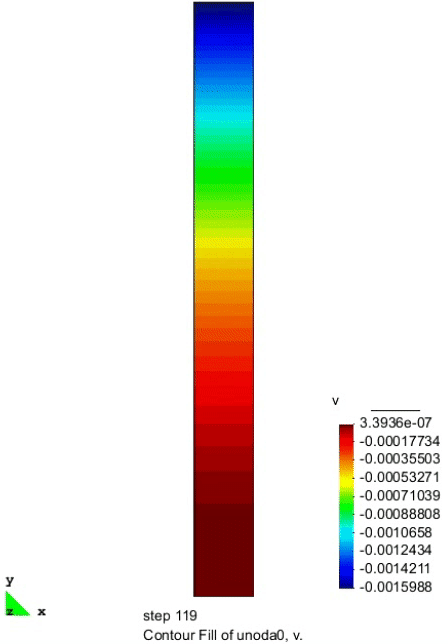
竖向位移的分布

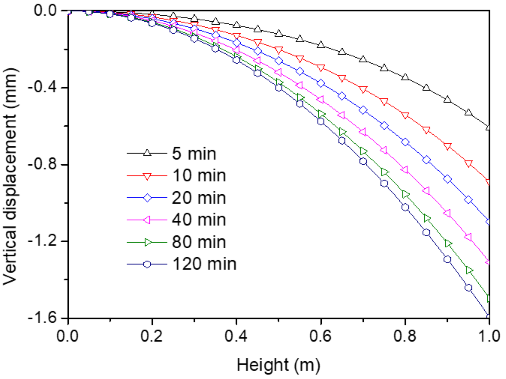
上图给出了不同时刻在砂柱中心线处纵向位移的分布情况。孔隙水的排出导致砂土内部的有效应力增大，进而发生沉降现象。排水 2 h 后砂柱表面的沉降达到了 1.6 mm，这与现有文献的计算结果是一致的。

部分模拟动画


孔隙水压力	孔隙气压力	竖向位移

参考文献

[1] Li W , Wei C .An efficient finite element procedure for analyzing three‐phase porous media based on the relaxed Picard method[J].International Journal for Numerical Methods in Engineering, 2015, 101(11).DOI:10.1002/nme.4830.