瞬态热传导问题的另类解法
关键词: 瞬态 线性 热传导 向后差分
如果要解锁有限元语言的高级应用技巧,就必须深刻理解 PDE 文件和 NFE 文件的关系。本节以瞬态热传导问题为例,展示在不使用 mass 语句的情况下,通过灵活运用 PDE 与 NFE 文件的语法规则,同样可以实现与标准算例完全一致的计算结果。
PDE 与 NFE 的关系梳理
同一个物理场的 PDE 和 NFE 文件之间的联系十分密切。这里我们首先来梳理一下 PDE 和 NFE 之间的数据传递机制,它们之间的数据传递过程大致上可以用下图来表示。
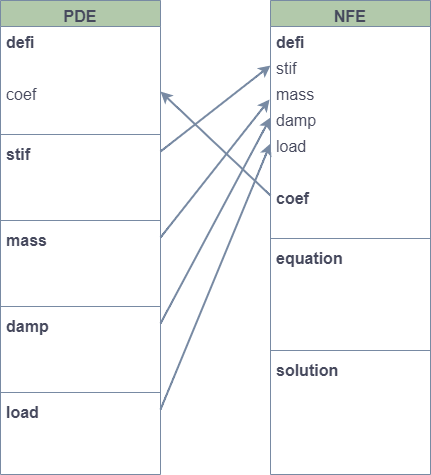
事实上, PDE 和 NFE 是浑然一体的。我们可以将 PDE 理解成 NFE 的一个子程序。我们在 PDE 文件中的 stif、mass、damp 和 load 信息段书写的内容,PDE 会将其转化为单元矩阵的信息,并传递给 NFE 文件。而 NFE 则继续将 PDE 提供的单元矩阵组装成为总体矩阵。此外,NFE 还可以根据 PDE 的具体需要, 通过 coef 语句向其传递生成单元矩阵所可能要用到的场变量的数据。注意到在 PDE 和 NFE 中都存在的 coef 语句,它实际上是扮演了数据通道的角色。你会发现, coef 语句在瞬态问题、非线性问题、多场耦合问题和算子分裂问题等领域有着大量的应用,发挥了至关重要的作用。
需要补充说明的是,由于 FBC 和 PDE 文件大同小异,上面对 PDE 文件所阐述的内容对 FBC 文件同样适用,我们不再作单独地论述。
控制方程
实践出真知,体验需力行。我们以瞬态热传导问题为例,换一个思路重新来求解一下。下面你将会看到,我们通过改写 PDE 和 NFE 文件,只用 stif 信息段和 load 信息段,而不用 mass 信息段,同样能够实现之前标准算例的计算结果。
回顾之前的章节,对于二维直角坐标系,瞬态热传导服从如下偏微分方程 \(\rho c \frac{\partial u}{\partial t}-\frac{\partial}{\partial x}\left(k \frac{\partial u}{\partial x}\right)-\frac{\partial}{\partial y}\left(k \frac{\partial u}{\partial y}\right)=\rho Q\ \left(\text{in } \Omega\right) \tag{1}\label{eq1}\) 其中,$\rho$ 表示材料密度,$c$ 为材料的比热,$u$ 表示温度,$k$ 是热传导系数,$Q$ 为热源密度,$x$ 和 $y$ 为二维直角坐标系下的坐标变量,$t$ 为时间。
我们只考虑第一类边界条件,则上式对应的弱形式为 \(\int_{\Omega} \rho c \frac{\partial u}{\partial t} \delta u d \Omega+\int_{\Omega}\left(k \frac{\partial u}{\partial x} \frac{\partial \delta u}{\partial x}+k \frac{\partial u}{\partial y} \frac{\partial \delta u}{\partial y}\right) d \Omega=\int_{\Omega} \rho Q \delta u d \Omega \tag{2}\label{eq2}\) 在此基础上,继续采用向后差分法进行时域离散,可将上式改写为 \(\int_{\Omega} \rho c \frac{u^{n+1}-u^{n}}{\Delta t} \delta u^{n+1} d \Omega+\int_{\Omega}\left(k \frac{\partial u^{n+1}}{\partial x} \frac{\partial \delta u^{n+1}}{\partial x}+k \frac{\partial u^{n+1}}{\partial y} \frac{\partial \delta u^{n+1}}{\partial y}\right) d \Omega=\int_{\Omega} \rho Q \delta u^{n+1} d \Omega\) 其中,上标 $n$ 表示时间步数,$\Delta t$ 为时间步长。将上式整理后得到 \(\rho c \int_{\Omega} u^{n+1}\delta u^{n+1} d \Omega+{\Delta t} \int_{\Omega}\left(k \frac{\partial u^{n+1}}{\partial x} \frac{\partial \delta u^{n+1}}{\partial x}+k \frac{\partial u^{n+1}}{\partial y} \frac{\partial \delta u^{n+1}}{\partial y}\right) d \Omega\\={\Delta t} \int_{\Omega} \rho Q \delta u^{n+1} d \Omega+\rho c \int_{\Omega}u^n\delta u^{n+1} d \Omega \tag{3}\label{eq3}\) 对于式 $\eqref{eq3}$,我们将整个方程的左端作为刚度矩阵项,右端作为荷载项。进行空间离散化后,可进一步写成矩阵形式
\(KU=F \tag{4}\label{eq4}\) 其中,$K$ 为刚度矩阵,$U$ 为温度向量,$F$ 为载荷向量。该式即为最终需要求解的线性方程组。
公式推导完毕,接下来就可以写脚本文件了。
脚本编写
我们知道,一个具体问题的有限元语言表述,通常需要包含 5 种类型的文件:PDE、FBC、MDI、GCN 和 NFE。由于方程 $\eqref{eq3}$ 不存在边界积分项,所以这里不需要写 FBC 文件。MDI、GCN 可参考之前瞬态热传导问题的章节,变化不大。为了便于对比,我们仍将项目命名为 lp,下面仅给出关键的 PDE 和 NFE 文件的详细介绍。
PDE 文件
根据有限元语言的语法规则,将方程 $\eqref{eq3}$ 的体积分项写入 PDE 文件如下。
| heat.pde | 说明 |
|---|---|
| defi disp u coor x y shap %1 %2 gaus %3 coef un mate rho ec ek eq 5e3; 1e1; 1e2; 0.0 $c6 rc = rho*ec stif dist = +[u;u]*rc +[u/x;u/x]*ek*dt+[u/y;u/y]*ek*dt load = +[u]*rho*eq*dt+[u]*{un}*rc end |
系统关键字(信息定义) 定义未知量 定义坐标分量 定义采用的形函数 定义采用的积分方式 声明从 NFE 接收到的变量 定义用到的材料参数和默认参数值 计算热容参数 (空行) 系统关键字(单元刚度矩阵表达式定义) 刚度矩阵项,对应式 $\eqref{eq3}$ 左侧 (空行) 荷载向量项,对应式 $\eqref{eq3}$ 右侧 (空行) 系统关键字(文件结束) |
这里将 shap 和 gaus 行的参数设为待定,参数值 %1、%2 和 %3 将从 MDI 文件中取得。
NFE 文件
我们在 parb.nfe 模板文件的基础上稍作修改,得到了以下的 lpa.nfe 文件。
| lpa.nfe | 说明 |
|---|---|
| defi stif s load f coef u equation vect u read(s,unod) u matrix = [s] forc = [f] solution u write(s,unod) u gidpost("u",time) u(1) end |
DEFI段 定义刚度矩阵名为 s 定义载荷向量名为 f 声明要向 PDE 传送的场向量 (空行) EQUATION段 定义场向量 读入上一时间步的场向量值 方程组左端矩阵 方程组右端向量 (空行) SOLUTION段 定义求解的场向量 临时存储当前的结果,供下一时间步读取 将计算结果写入 GiD 后处理文件 (空行) 结束标记 |
这里需要重点关注的是场向量值 u 的传递过程。仔细观察后发现,我们在 nfe 文件中,总共对 u 执行了以下 6 步操作:
- 通过 vect 语句声明场向量值 u
- 由 read 语句从临时文件读入上一时间步的数据,即对 u 进行赋值
- 通过 coef 语句将 u 传递给了 PDE 文件,用于单元矩阵的生成
- 通过 solution 语句计算,得到当前时间步的计算结果, 对 u 重新赋值
- 由 write 语句将 u 写入临时文件,即对 u 进行存储
- 由 gidpost 语句将 u 写入 GiD 后处理文件
上述每一步操作都必不可少。这里的整个 NFE 文件可以说没有一行是多余的。如果你善于总结,会发现对于大部分的瞬态问题和非线性问题,都是按与此类似的步骤传递数据的。用户可以进一步结合 PDE 和 NFE 文件的语法文档和其他相关算例,深刻体会一下其中的逻辑体系。
后续的编译测试过程留给用户自行完成,这里不再给出。
需要提醒的是,当时间步长很小时,与之前提供的标准算例的计算结果可能会有较大差别。这其实是由质量矩阵形式的不同造成的。当前算例本质上是在 stif 信息段使用了分布式的质量矩阵。分布式与集中式的质量矩阵的作用效果是有差异的。这是一个宏大的话题,感兴趣的读者可自行查阅相关文献。
小结
至此,大功告成。对比我们之前提供的标准算例,这套新的脚本文件将原来的 mass 信息段的内容融入到了 stif 信息段和 load 信息段中,同样实现了瞬态热传导问题的求解。两者的主要不同之处其实是在于时域离散和空间离散的顺序。前者是先进行空间离散,得到矩阵形式,再用向后差分法进行时域离散。这里正好相反,先进行的时域离散,后进行的空间离散。这样就将部分原本应由 NFE 文件做的事情,转移到了 PDE 文件中。
如果充分理解了 PDE 和 NFE 文件之间的联系,能够做到举一反三,那你就可以放心大胆地应用有限元语言和 FEtch 系统,去求解其他更复杂的问题了。





