Biot 固结问题
关键词: 瞬态 线性 Biot固结 向后差分 流固耦合 全耦合
近年来,多孔介质流固耦合问题越来越受到人们的重视。它在很多工程领域都有广泛的应用,如软土地基固结沉降,地下流体开采所导致的地面沉降,煤层气的耦合渗流和突出,边坡和坝基的稳定性问题,城市垃圾填埋及核废料处理,生物体软组织变形研究,等等。
多孔介质流固耦合理论源自 Biot 的饱和土固结理论,之后进行的涉及到各个领域的流固耦合模型的研究及应用基本上都是以 Biot 固结理论为基础的,差别之处可能在于介质本构关系不同,孔隙流体饱和或非饱和的差别,以及有效应力原理形式的不同。
本节以二维饱和土体的 Biot 固结问题为例,讲解如何使用 FEtch 系统对多孔介质流固耦合问题进行全耦合求解。
控制方程
微分形式
平衡方程
二维直角坐标系下,不考虑固体骨架和孔隙流体的压缩性,忽略惯性力和体力的作用,准静态的 Biot 方程可写成如下较为简单的形式 \(\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \sigma_{x y}}{\partial y}-\frac{\partial p}{\partial x} = 0 \ \left(\text{in } \Omega\right) \tag{1}\label{eq1}\) \(\frac{\partial \sigma_{x y}}{\partial x}+\frac{\partial \sigma_{y y}}{\partial y}-\frac{\partial p}{\partial y} = 0\ \left(\text{in } \Omega\right) \tag{2}\label{eq2}\) \(\frac{\partial \epsilon}{\partial t}-\frac{\partial}{\partial x}\left(\frac{k}{\gamma_w} \frac{\partial p}{\partial x}\right)-\frac{\partial}{\partial y}\left(\frac{k}{\gamma_w} \frac{\partial p}{\partial y}\right)=0 \ \left(\text{in } \Omega\right) \tag{3}\label{eq3}\)
几何方程 \(\varepsilon_{xx}=\frac{\partial u}{\partial x},\quad \varepsilon_{yy}=\frac{\partial v}{\partial y},\quad \varepsilon_{x y}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x},\quad\epsilon=\varepsilon_{xx}+\varepsilon_{yy}\) 本构方程(平面应变) \(\left(\begin{array}{c}\sigma_{x x} \\ \sigma_{y y} \\ \sigma_{x y} \end{array}\right)=\frac{E}{(1+\nu)(1-2\nu)}\left(\begin{array}{ccc} 1-\nu & \nu & 0 \\ \nu & 1-\nu & 0 \\ 0 & 0 & 0.5-\nu \end{array}\right)\left(\begin{array}{l} \varepsilon_{x x} \\ \varepsilon_{y y} \\ \varepsilon_{x y} \end{array}\right)\) 以上式子可以简记为 \(\nabla\cdot(\boldsymbol{\sigma}-p\boldsymbol{I})=\boldsymbol{0}\ \left(\text{in } \Omega\right)\) \(\frac{\partial \epsilon}{\partial t}-\nabla\cdot \frac{k}{\gamma_w}\nabla p=\boldsymbol{0} \ \left(\text{in } \Omega\right)\) \(\boldsymbol{\varepsilon}=\left(\nabla \boldsymbol{u}+\nabla^{T} \boldsymbol{u}\right)/2,\quad\epsilon =\boldsymbol{\varepsilon}:\boldsymbol{I}\) \(\boldsymbol{\sigma}=\boldsymbol{D} \boldsymbol{\varepsilon}\) 其中, $u$、$v$ 为位移 $\boldsymbol{u}$ 的分量,$p$ 为孔压(以压为正)。 $\varepsilon_{x x}$、$\varepsilon_{y y}$ 、 $\varepsilon_{x y}$ 为应变 $\boldsymbol{\varepsilon}$ 的分量,$\epsilon$ 为体应变,$\sigma_{x x}$ 、$\sigma_{y y}$ 、$\sigma_{x y}$ 为有效应力 $\boldsymbol{\sigma}$ 的分量。$\nabla$ 为梯度算子,$\boldsymbol{D}$ 为刚度矩阵,$\boldsymbol{I}$ 为单位矩阵。参数 $E$ 为弹性模量, $\nu$ 为泊松比,$k$ 为渗透系数,$\gamma_w$ 为水的容重。 $x$、$y$ 为直角坐标系下的坐标分量。
边界条件
考虑两类边界条件:
第一类边界条件,给定位移和孔压 \(u=u_0,\ v=v_0,\ p=p_0\ \left(\text{on } \Gamma_1\right)\)
第二类边界条件,给定外力和流量 \(T_{x}=\left(\sigma_{x x}-p,\sigma_{x y}\right)\cdot \mathbf{n}=t_x,\\ T_{y}=\left(\sigma_{x y},\sigma_{y y}-p\right)\cdot \mathbf{n}=t_y,\\ \frac{k}{\gamma_w}\frac{\partial u}{\partial \mathbf{n}} \cdot \mathbf{n}=q_0\ \left(\text{on } \Gamma_2\right)\)
其中,$u_0$ 、$v_0$ 为边界上的位移, $p_0$ 为边界上的孔压;$T_{x}$、$T_{y}$ 分别为边界上的外力在 $x$ 和 $y$ 方向的分量,$q_0$ 为边界上的流量(以流入为正)。$\mathbf{n}$ 为边界上的单位外法向量。
弱形式
PDE 文件的编写依赖于待解偏微分方程的弱解方程。根据虚位移原理,对力学平衡方程 $\eqref{eq1}$ 和 $\eqref{eq2}$ 两边分别乘以位移的变分并在求解区域内积分,得到其等效积分形式 \(\int_{\Omega}\left[\left(\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \sigma_{x y}}{\partial y}-\frac{\partial p}{\partial x}\right) \delta u+\left(\frac{\partial \sigma_{x y}}{\partial x}+\frac{\partial \sigma_{y y}}{\partial y}-\frac{\partial p}{\partial y}\right) \delta v\right] d\Omega=0\) 对上式进行分部积分,并代入边界条件,得到弱形式 \(\int_{\Omega}\left(\sigma_{x x} \delta \varepsilon_{x x}+\sigma_{y y} \delta \varepsilon_{y y}+\sigma_{x y} \delta \varepsilon_{x y}\right)d\Omega -\int_{\Omega}p\delta \epsilon d\Omega =\int_{\Gamma_2}\left(t_{x} \delta u+t_{y} \delta v\right) d\Gamma \tag{4}\label{eq4}\)
将本构方程代入上式,即可得到以位移为基本未知量的弱形式。
对渗流方程 $\eqref{eq3}$ 两边分别乘以孔压的变分并在全域上积分,得 \(\int_{\Omega}\left[\frac{\partial \epsilon}{\partial t}-\frac{\partial}{\partial x}\left(\frac{k}{\gamma_w} \frac{\partial p}{\partial x}\right)-\frac{\partial}{\partial y}\left(\frac{k}{\gamma_w} \frac{\partial p}{\partial y}\right)\right] \delta p d \Omega=0\) 对于二阶导数的部分,利用分部积分将其中的一阶导数转化到孔压的变分上,并继续代入边界条件,得 \(\int_{\Omega}\frac{\partial \epsilon}{\partial t} \delta p d \Omega+\int_{\Omega}\left(\frac{k}{\gamma_w} \frac{\partial p}{\partial x} \frac{\partial \delta p}{\partial x}+\frac{k}{\gamma_w} \frac{\partial p}{\partial y} \frac{\partial \delta p}{\partial y}\right) d \Omega=\int_{\Gamma_2} q_{0} \delta p d \Gamma \tag{5}\label{eq5}\) 这就是孔压场的最终的弱解形式。
离散化
对式 $\eqref{eq4}$ 和 $\eqref{eq5}$ 进行空间离散化后,可进一步写成矩阵形式 \(M \dot{U}+SU=F\) 其中, $U$ 为位移和孔压的组合向量 $[\ u\ \ v\ \ p\ ]^T$,$\dot{U}$ 为组合向量 $U$ 对时间的导数向量,$M$ 为质量矩阵, $S$ 为刚度矩阵,$F$ 为载荷向量。采用向后差分法进行时域离散,可将上式改写为 \(M \frac{U^{t+\Delta t}-U^{t}}{\Delta t}+S U^{t+\Delta t}=F^{t+\Delta t}\) 整理得 \((M+S \Delta t) U^{t+\Delta t}=F^{t+\Delta t} \Delta t+M U^{t} \tag{6}\label{eq6}\) $\Delta t$ 为时间步长,上标 $t+\Delta t$ 代表当前时间步,$t$ 代表上一时间步。该式即为最终需要求解的线性方程组。
注意,这里最终的线性方程组不是对称的,需使用非对称求解器,计算量较大。理论上,可以通过对时间求导,将力学平衡方程转化成增量形式,再经过适当变换,实现线性方程组的对称化。有兴趣的用户可以自行练习操作。
脚本编写
一个具体问题的有限元语言表述,通常需要包含 5 种类型的文件:PDE、FBC、MDI、GCN 和 NFE。下面依次给出详细介绍。
PDE 和 FBC 文件
在这个例子中,采用全耦合的方法,将位移和孔压视为同一个物理场。根据有限元语言的语法规则,将方程 $\eqref{eq4}$ 和 $\eqref{eq5}$ 的体积分项写入 PDE 文件如下。
| uvp.pde | 说明 |
|---|---|
| defi disp u,v,p coor x,y shap %1 %2 gaus %3 func ex,ey,exy,evv mate pe pv pk pw 4e6;0.25;8.64e-12 $c6 fact = pe/(1.+pv)/(1.-2.*pv) $c6 ek = pk/pw func ex=+[u/x] ey=+[v/y] exy=+[u/y]+[v/x] evv=+[u/x]+[v/y] stif dist= +[ex;ex]*fact*(1.-pv) +[ex;ey]*fact*(pv) +[ey;ex]*fact*(pv) +[ey;ey]*fact*(1.-pv) +[exy;exy]*fact*(0.5-pv) -[p;evv] +[p/x;p/x]*ek+[p/y;p/y]*ek mass dist=+[evv;p] load=+[u]*0.0 end |
系统段落关键字(信息定义) 定义未知量 定义坐标分量 定义采用的形函数 定义采用的积分方式 定义函数用于表达应变 定义用到的材料参数和参数值 参数自定义和计算 (空行) 系统段落关键字(向量函数表达式) $\varepsilon_{x x}$ (空行) $\varepsilon_{y y}$ (空行) $\varepsilon_{x y}$ (空行) $\epsilon$ (空行) 系统段落关键字(单元刚度矩阵表达式) 刚度矩阵项 对应式 $\eqref{eq4}$ 左侧第 1 项 对应式 $\eqref{eq4}$ 左侧第 2 项 对应式 $\eqref{eq5}$ 左侧第 2 项 (空行) 系统段落关键字(单元质量矩阵表达式) 质量矩阵项,对应式 $\eqref{eq5}$ 左侧第 1 项 (空行) 荷载向量项,为零矩阵 (空行) 系统关键字(文件结束) |
这里将 shap 行和 gaus 行的参数设为待定,参数值 %1、%2 和 %3 将从 MDI 文件中取得。
同样地,将方程 $\eqref{eq4}$ 和 $\eqref{eq5}$ 的的边界积分项写入 FBC 文件如下。
| uvp.fbc | 说明 |
|---|---|
| defi disp u v p coor x shap %1 %2 gaus %3 mate fx fy ep 0.0;1e3;0.0; stif dist = +[u;u]*0.0 load = +[u]*fx+[v]*fy+[p]*ep end |
系统段落关键字(信息定义) 定义未知量 定义坐标分量 定义采用的形函数 定义采用的积分方式 定义用到的材料参数和参数值 (空行) 系统段落关键字(单元刚度矩阵表达式定义) 刚度矩阵项,为零矩阵 (空行) 荷载向量项,对应式 $\eqref{eq4}$ 和 $\eqref{eq5}$ 右侧 (空行) 系统关键字(文件结束) |
MDI 文件
MDI 文件负责组织 PDE 和 FBC 文件,声明程序具体使用的坐标系统、单元类型和积分方法。这里文件命名为 biot.mdi,具体内容如下。
| biot.mdi | 说明 |
|---|---|
| 2dxy #a 1 3 u v p pde uvp q8g3 fbc uvp l3g3 # |
在二维直角坐标系下求解 a场,1 个初值,1 个自由度,自由度名称为 u 调用 uvp.pde,采用 8 节点二次四边形单元,3 点高斯积分 调用 uvp.fbc,采用 8 节点二次线单元,3 点高斯积分 (文件结束符,可留空) |
注意,同一个场的 PDE 和 FBC 的单元类型和积分方法需要保证匹配,否则会导致计算精度降低,甚至计算失败的情况发生。MDI 文件声明的单元类型和积分方式将以参数的形式传递给 PDE 和 FBC 文件中的的 %1、%2 和 %3。如果后续想要使用其他的单元类型或者积分方法,只需修改 MDI 文件即可。
GCN 文件
GCN 文件给出计算流程信息,系统规定其文件名字要与 MDI 文件一致。准静态Biot方程属于线性抛物方程,计算流程比较简单,包含一个时间步的循环过程。只需填写少量代码,对应的 GCN 文件如下。
| biot.gcn | 说明 |
|---|---|
| defi a parb open(1,file='time.dat') read(1,*) dt,tmax,factor close(1) #startnin a time = 0.0 do while (time <= tmax-1d-8) time = time + dt if (time > tmax) then dt = dt-(time-tmax) time = tmax endif #solvnin a dt = dt*factor enddo |
算法引入段 场 a,采用的算法模板文件为 parb.nfe (空行) 命令流段 从 time.dat 文件读取时间步参数 factor用于动态调整时间步长 初始化 a 场 对 time 赋初始值 循环开始 更新 time 越界修正 求解 a 场 变更时间步长,factor倍 循环结束 |
注意:由于单元质量矩阵和刚度矩阵的不对称,导致最终的代数方程组左端矩阵不是对称的,所有这里采用了非对称求解器 nin。
NFE 文件
由 GCN 文件可知,a 场使用了 parb 算法。初始化后,系统基于模板文件自动生成了 biota.nfe 文件。这里需要修改的是 gidpost 输出语句:
- 位移(矢量)和孔压(标量)在物理本质上是两个场,在将结果保存到 GiD 后处理文件时需要进行区分,即采用两次 gidpost 语句,分开输出。
修改完成后的文件内容如下。
| biota.nfe | 说明 |
|---|---|
| defi stif s mass m load f equation vect u read(s,unod) u matrix = [s]*dt+[m] forc = [f]*dt+[m]*[u] solution u write(s,unod) u gidpost("u v",time) u(1),u(2) gidpost("p",time) u(3) end |
DEFI段 定义刚度矩阵名为 s 定义质量矩阵名为 m 定义载荷向量名为 f (空行) EQUATION段 定义场向量 读入上一时间步的场向量值 方程组左端矩阵,对应式 $\eqref{eq6}$ 左侧 方程组右端向量,对应式 $\eqref{eq6}$ 右侧 (空行) SOLUTION段 定义求解的场向量 临时存储当前的结果,供下一时间步读取 将位移结果写入 GiD 后处理文件 将孔压结果写入 GiD 后处理文件 (空行) 结束标记 |
算例1
Tezaghi 固结
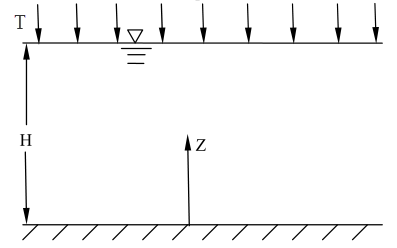
Tezaghi 固结问题是土力学的经典算例。考虑厚度为 $H=1.0\ \mathrm{m}$ 的饱和含水层,水平方向为无限长。底面为不透水边界,顶面为渗流自由面,孔隙压力 $p=0$;含水层材料为各向同性,其弹性模量 $E=5.0×10^8\ \mathrm{Pa}$,泊松比 $\nu=0.3$ ,渗透系数 $k=10^{-8}\ \mathrm{m/s}$,水的容重为 $\gamma_w = 10^4\ \mathrm{N/m^3}$。顶面突然施加 $T=10^4\ \mathrm{Pa}$ 的均布载荷。不计重力影响。求 1 小时后土体的变形情况和孔压分布。
前处理
填写材料参数文件
系统自动生成了 biot.mat 文件,用于设置材料参数。参数初始值全部为 PDE 和 FBC 文件给出的默认值。可根据具体问题进行修改。对于本算例,修改完成后的文件内容如下。
| biot.mat | 说明 |
|---|---|
| 1 5 aeq8g3 num pe pv pk pw 1 5.0e8 0.3 1e-8 1e4 # 1 4 all3g3 num fx fy ep 1 0.0 1e4 0.0 # |
8 节点四边形面单元 材料参数 参数值 分隔符 3 节点线形边界单元 材料参数 参数值 分隔符 |
填写时间步文件
由 biot.gcn 文件可知,用户自定义了时间步长文件 time.dat,给出时间步长和终止时间。文件内容如下:
1 3600 1.05
可知, 初始时间步长为 1 s,结束时间为 3600 s,时间步长放大因子为 1.05。
注意:Biot 问题的数值方法对时间步长的下限有要求,不能太小,否则容易发生数值震荡现象。具体理论请查看相关文献。
赋单元材料
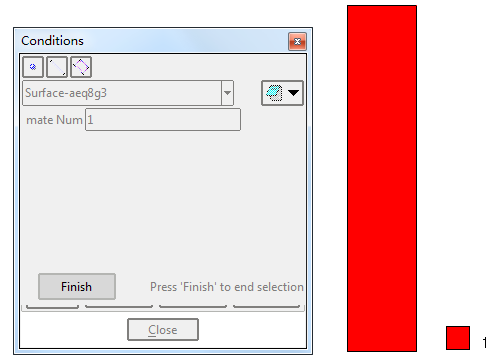
赋初始条件
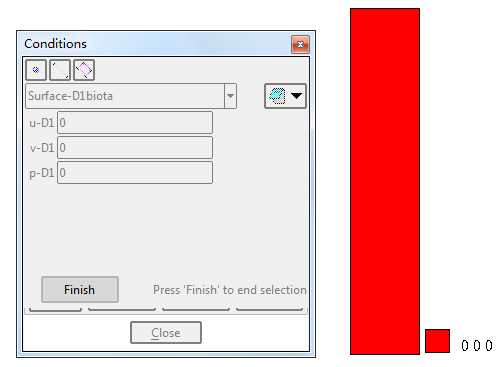
施加第一类边界条件
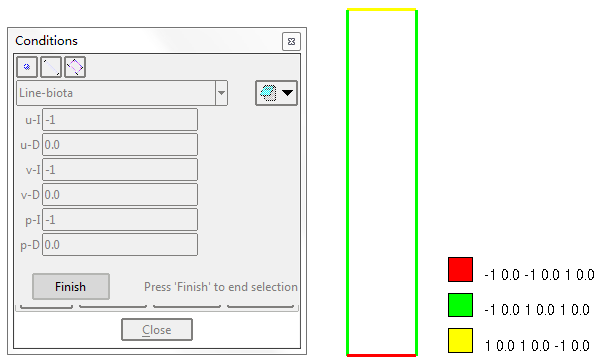
其中:
u-I 为边界类型,-1 表示约束,1 表示自由
u-D 为相应的约束值或施加节点力
由于有不同的边界条件交接,角点位置上的边界条件可能出现歧义。为此,继续明确定义角点处的边界条件。
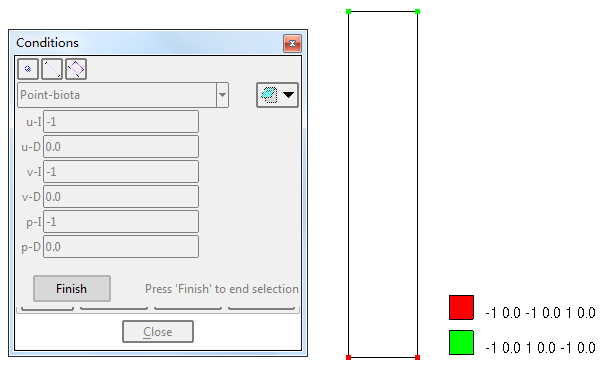
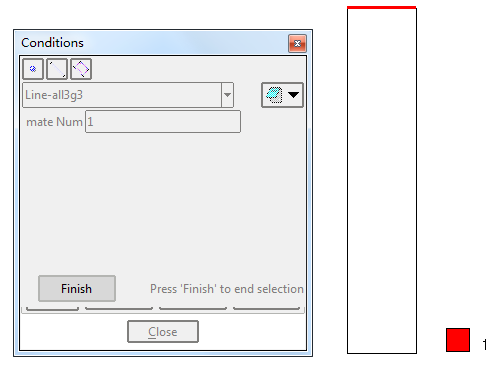
施加第二类边界条件
荷载作为第二类边界条件,以线单元的形式施加
网格剖分
根据所开发程序的计算要求,网格剖分采用 8 节点等参单元。共使用了 40 个单元,165 个节点。

计算结果
通过自动改变时间步长,变化范围从 1 s 到 167 s,总共使用了 107 个时间步。对计算结果稍加整理,效果如下。
竖向位移的演化过程
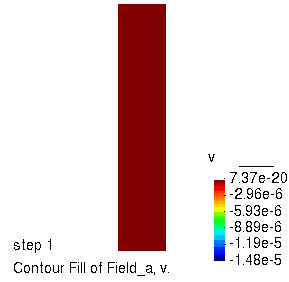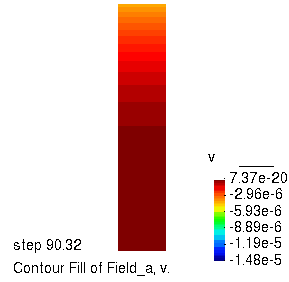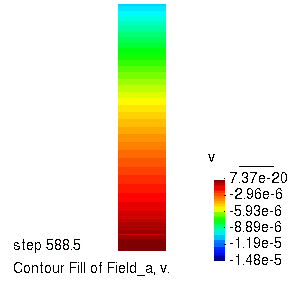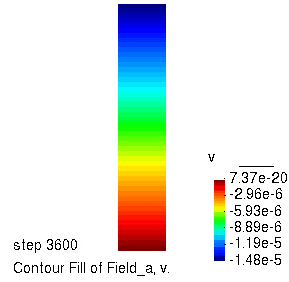
孔压的演化过程
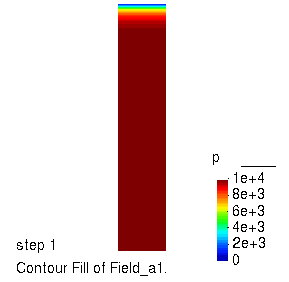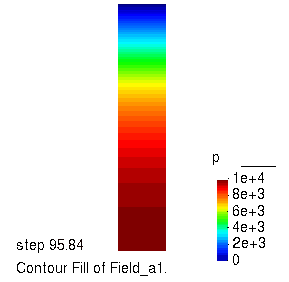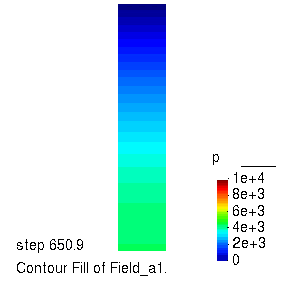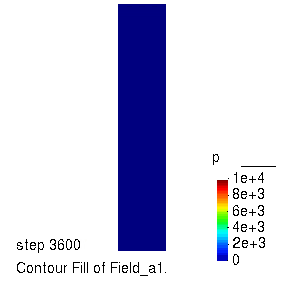
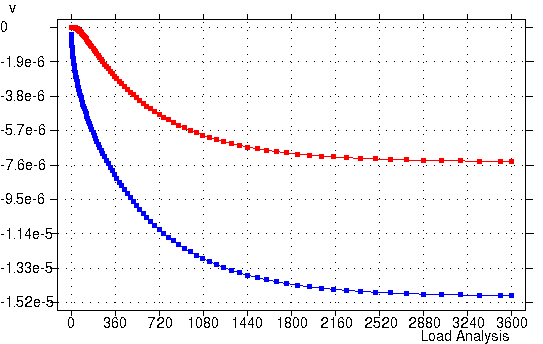
不同深度处位移随时间的变化曲线
土体表面(蓝线)和 0.5 m深处(红线)的位移情况如下图所示,反映了外力作用下土体逐渐压缩的过程。
不同高度处孔压随时间的变化曲线
选取深度为 0.1、0.3、0.5、0.7 和 0.9 m的位置作为观察点,孔压随时间变化的情况如下图所示。
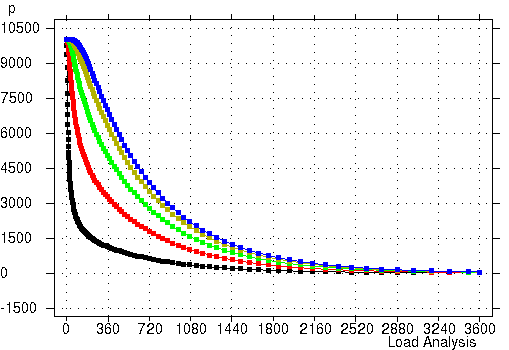
进一步分析可以发现数值解与解析解符合得很好,进而证明算法和程序的有效性。这里不再给出具体过程,留给用户自行验证。
算例2
圆柱土体固结
一个半径为 $R = 1.0\ \mathrm{m}$ 的无限长圆柱土体,在其外边界突然施加 $T = 10^4\ \mathrm{Pa}$ 的均匀径向压缩载荷。圆柱体表面为渗流自由面,孔隙压力 $p=0$。材料参数取值同算例 1。不计重力的影响。求 1 小时后土体的位移和孔压分布。
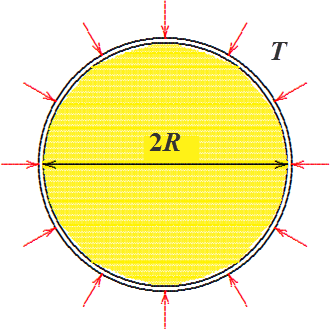
前处理
根据圆截面的对称性,取四分之一的区域进行模拟。
填写材料参数文件
由荷载和材料参数与算例 1 完全一致,这里直接使用算例 1 的 mat 文件。
填写时间步文件
同算例 1。
赋单元材料
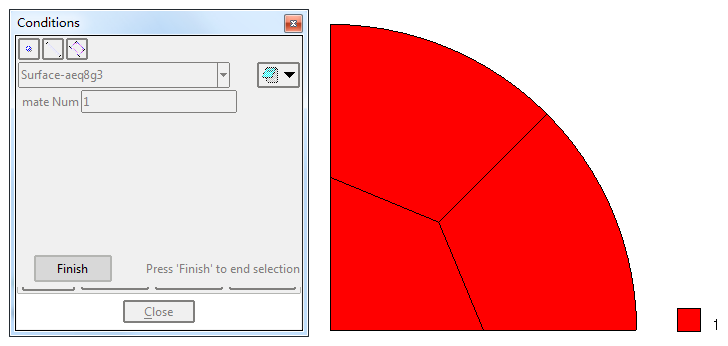
赋初始条件
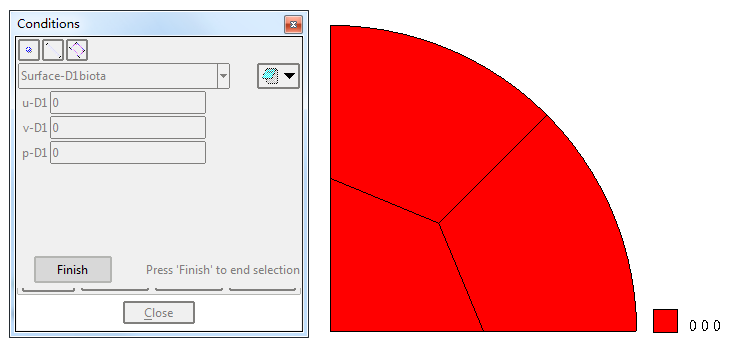
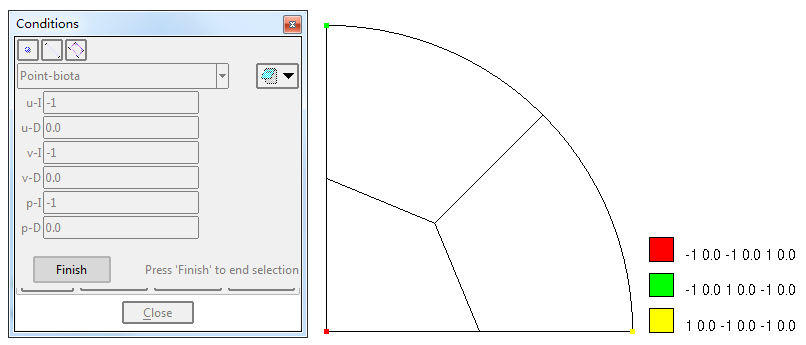
施加第一类边界条件
其中:
u-I 为边界类型,-1 表示约束,1 表示自由
u-D 为相应的约束值或施加节点力
由于有不同的边界条件交接,角点位置上的边界条件可能出现歧义。为此,继续明确定义角点处的边界条件。
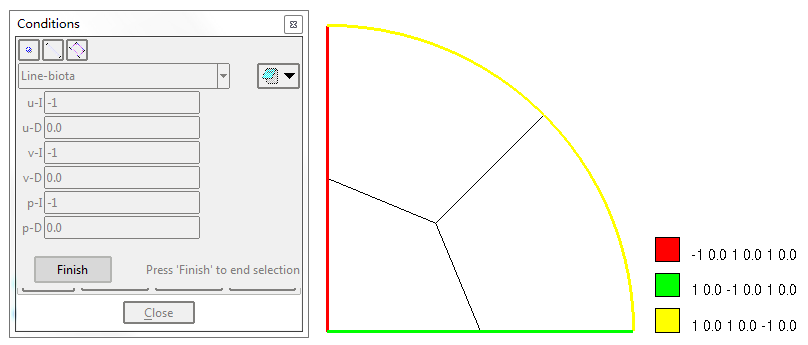
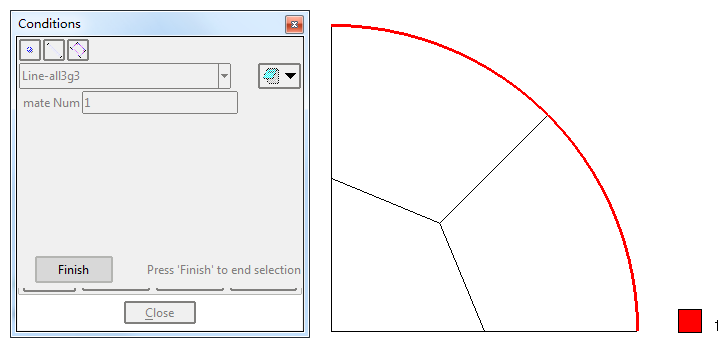
施加第二类边界条件
荷载作为第二类边界条件,以线单元的形式施加
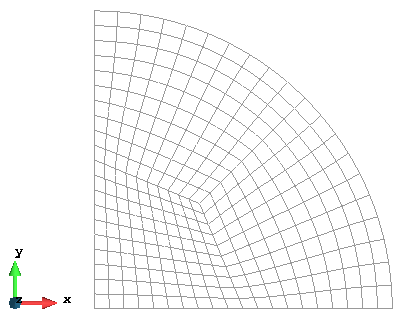
网格剖分
根据所开发程序的计算要求,网格剖分采用 8 节点等参单元。共使用了 300 个单元,961 个节点。
计算结果
通过自动改变时间步长,变化范围从 1 s 到 167 s,总共使用了 107 个时间步。对计算结果稍加整理,效果如下。
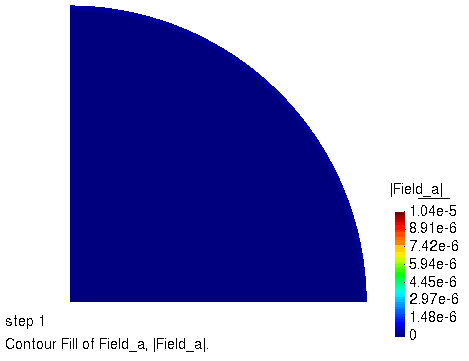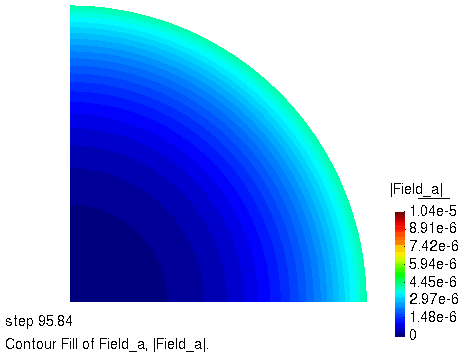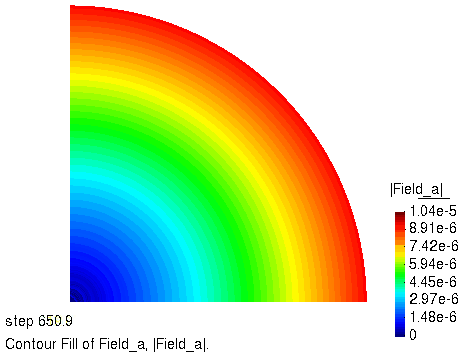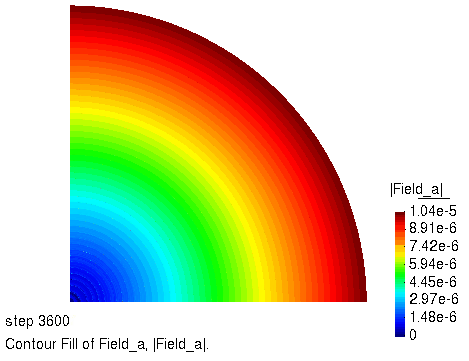
径向位移的演化过程
径向位移 $r=\sqrt{u^2+v^2}$,随时间的变化过程如下图所示。
孔压的演化过程
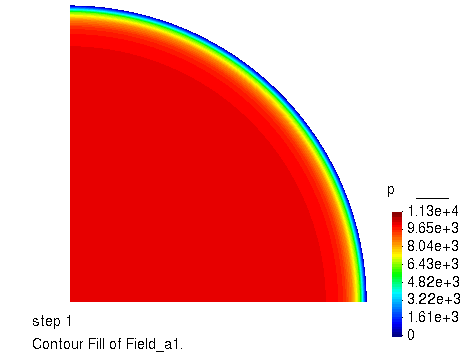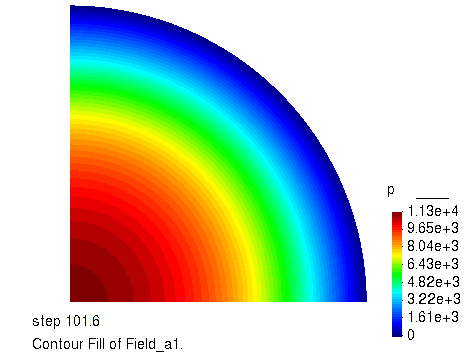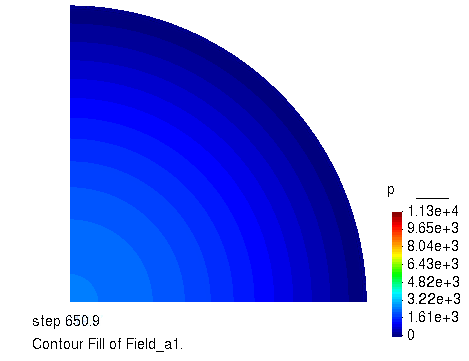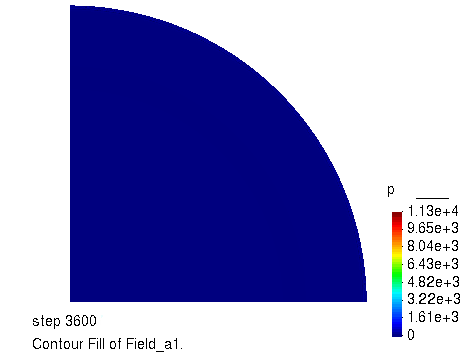
径向位移随时间的变化曲线
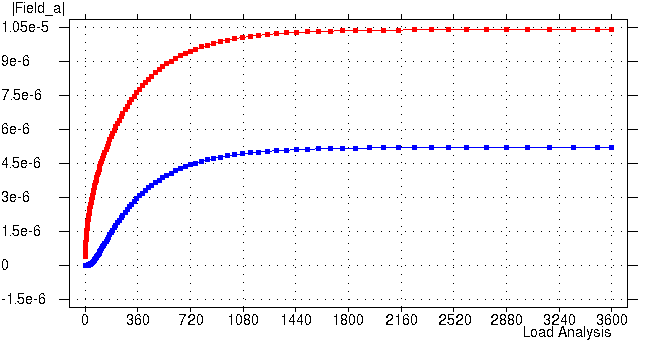
土体表面(红线)和 0.5 m 深处(蓝线)的径向位移情况如下图所示,反映了土体整体逐渐压缩的过程。
孔压随时间的变化曲线
选取径向距离 0.0、0.4 和 0.8 m 的三个位置作为观察点,孔压随时间变化的情况如下图所示。
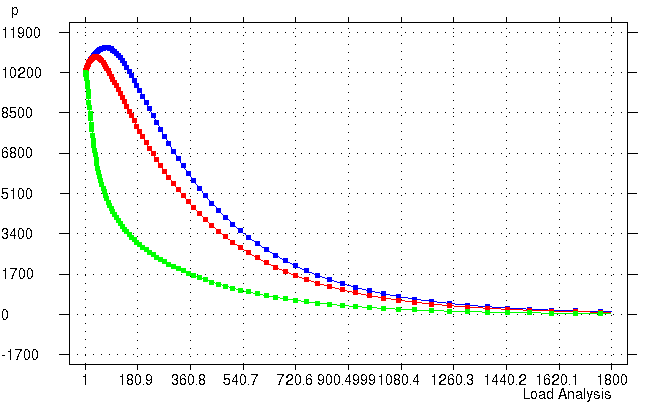
可以发现,较深位置的孔压有先上升后下降的现象,这就是著名的 Mandel-Cryer 效应。
进一步分析可以发现数值解与解析解符合得很好,进而证明算法和程序的有效性。这里不再给出具体过程,留给用户自行验证。





