三维稳态热传导问题

关键词： 稳态 线性 热传导

前面介绍的算例基本都是二维的，那么三维的问题应该如何处理呢？对 FEtch 来说，将一个已测试成功的有限元程序从二维扩展到三维，通常是非常直接、非常简单的。这里将给出详细介绍。本节以入门级别的稳态热传导问题为例，讲解如何使用 FEtch 系统求解三维的线性椭圆型偏微分方程。

控制方程

微分形式

对于三维直角坐标系，稳态热传导过程服从如下偏微分方程 $$\frac{\partial}{\partial x}\left(k \frac{\partial u}{\partial x}\right)+\frac{\partial}{\partial y}\left(k \frac{\partial u}{\partial y}\right)+\frac{\partial}{\partial z}\left(k \frac{\partial u}{\partial z}\right)+Q=0\ \left(\text{in } \Omega\right) \tag{1}\label{eq1}$$ 其中，$u$ 表示温度，$k$ 是热传导系数，$Q$ 为热源密度，$x$ 、 $y$ 和 $z$ 为三维直角坐标系下的坐标变量。

这里考虑两类边界条件:

第一类边界条件，给定温度 $$u=\bar{u}\ \left(\text{on } \Gamma_1\right)$$

第二类边界条件，给定热流 $$k\frac{\partial u}{\partial \mathbf{n}} \cdot \mathbf{n}=q\ \left(\text{on } \Gamma_2\right)$$

其中，$\bar{u}$ 和 $q$ 为边界上的温度和热流值。$\mathbf{n}$ 为边界上的单位外法向量，热流以进入区域为正。

对比二维问题，三维情况主要有以下两点变化：

• 微分方程 $\eqref{eq1}$ 多了一项，是新增的关于 $z$ 坐标的二阶导数。
• 边界条件区域的几何类型发生了变化。对二维问题来说是线边界，对三维问题来说则是面边界了，升高了一维。

弱形式

运用虚位移原理求温度，由微分方程 $\eqref{eq1}$ 两端乘以温度的变分，并在全域上积分，得 $$\int_{\Omega}\left(\frac{\partial}{\partial x}\left(k \frac{\partial u}{\partial x}\right)+\frac{\partial}{\partial y}\left(k \frac{\partial u}{\partial y}\right)+\frac{\partial}{\partial z}\left(k \frac{\partial u}{\partial z}\right)+\ Q\right) \delta u d \Omega=0$$ 对于二阶导数的部分，利用分部积分将其中的一阶导数转化到温度的变分上，得 $$\int_{\Omega}\left(k \frac{\partial u}{\partial x} \frac{\partial \delta u}{\partial x}+k \frac{\partial u}{\partial y} \frac{\partial \delta u}{\partial y}+k \frac{\partial u}{\partial z} \frac{\partial \delta u}{\partial z}\right) d \Omega=\int_{\Omega} Q \delta u d \Omega+\int_{\Gamma} k \frac{\partial u}{\partial \mathbf{n}} \cdot \mathbf{n} \delta u d \Gamma$$ 对于分部积分得到的边界积分项，代入边界条件，得 $$\int_{\Omega}\left(k \frac{\partial u}{\partial x} \frac{\partial \delta u}{\partial x}+k \frac{\partial u}{\partial y} \frac{\partial \delta u}{\partial y}+k \frac{\partial u}{\partial z} \frac{\partial \delta u}{\partial z}\right) d \Omega=\int_{\Omega} Q \delta u d \Omega+\int_{\Gamma_2} q \delta u d \Gamma \tag{2}\label{eq2}$$ 这就是温度场的最终的弱解形式。对式 $\eqref{eq2}$ 进行空间离散化后，可进一步写成矩阵形式 $$SU=F$$ 其中，$S$ 为刚度矩阵，$U$ 为温度向量，$F$ 为载荷向量。该式即为最终需要求解的线性方程组。

脚本编写

一个具体问题的有限元语言表述，通常需要包含 5 种类型的文件：PDE、FBC、MDI、GCN 和 NFE。下面依次给出详细介绍。

PDE 和 FBC 文件

在这个例子中，只有一个物理场，需要给出温度场对应的 PDE 文件和 FBC 文件。根据有限元语言的语法规则，将方程 $\eqref{eq2}$ 的体积分项写入 PDE 文件如下。

同样地，将方程 $\eqref{eq2}$ 的边界积分项写入 FBC 文件如下。

对比二维算例可以发现，对应于控制方程弱形式 $\eqref{eq2}$ 的体积分项的变化，PDE 文件仅在 coor 语句和 stif 段添加了部分内容，改动不大。由于边界积分项的表达式未发生变化，所以 FBC 文件内容完全无需修改。

MDI 文件

MDI 文件负责组织 PDE 和 FBC 文件，声明程序具体使用的坐标系统、单元类型和积分方法。这里文件命名为 le3d.mdi，具体内容如下。

对比二维算例，MDI 文件仅做了少量更改：更新了坐标系语句，并选择了与之匹配的体单元和边界单元类型。仍然需要注意的是，同一个场的 PDE 和 FBC 的单元类型和积分方法需要保证匹配，否则会导致计算精度降低，甚至计算失败的情况发生。

GCN 文件

GCN 文件给出计算流程信息，系统规定其文件名字要与 MDI 文件一致。作为线性椭圆方程，三维稳态热传导问题的计算流程和二维问题相比是完全一样的，具体内容如下。

NFE 文件

GCN 文件使用了 ell 算法，系统会基于模板文件自动生成以下的 le3da.nfe 文件。

算例

问题描述

考虑尺寸为 $1.0\ \mathrm{m}\times1.0\ \mathrm{m}\times1.0\ \mathrm{m}$ 的正方体，热传导系数为 $1\ \mathrm{W}/\mathrm{m}/{ }^{\circ}\mathrm{C}$，内热源密度为 $0$。以三维直角坐标系建模，正方体位于区域 $\left[0,1\right]\times\left[0,1\right]\times\left[0,1\right]$ 内。它的六个面分别满足以下边界条件 $$u(0,y,z)=y+z\ \left(\text{ on } x=0\right)\\u(x,0,z)=x+z\ \left(\text{ on } y=0\right)\\u(x,y,0)=x+y\ \left(\text{ on } z=0\right)\\u(1,y,z)=1+y+z\ \left(\text{ on } x=1\right)\\u(x,1,z)=1+x+z\ \left(\text{ on } y=1\right)\\u(x,y,1)=1+x+y\ \left(\text{ on } z=1\right)$$ 求温度场的分布。

前处理

填写材料参数文件

系统自动生成了 le3d.mat 文件，用于设置材料参数。参数初始值全部为 PDE 和 FBC 文件给出的默认值。可根据具体问题进行修改。对于本算例，修改完成后的文件内容如下。

赋单元材料号

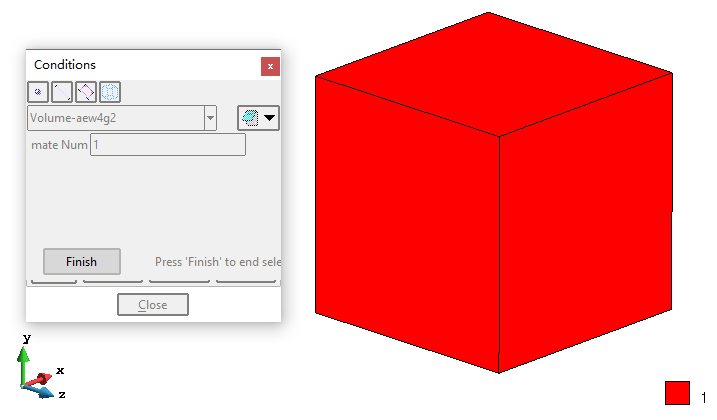
施加边界条件

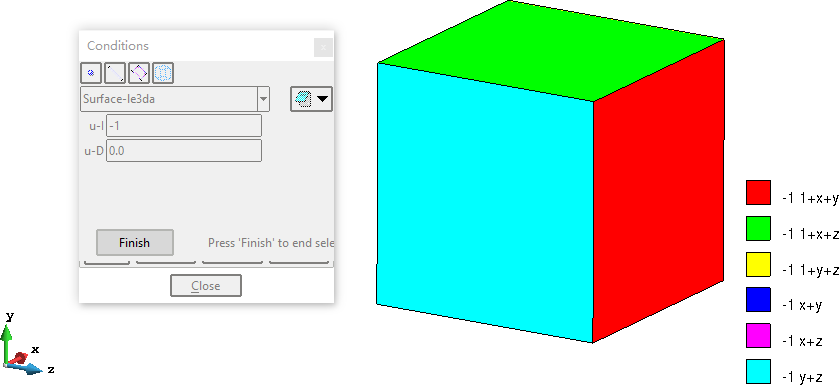
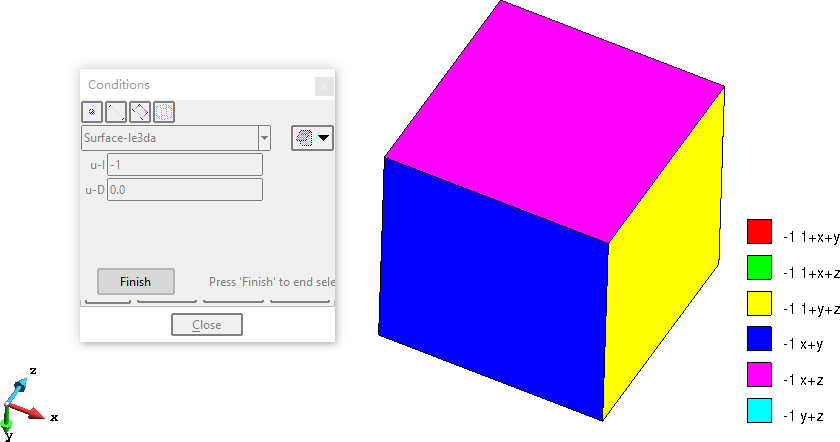
网格剖分

根据所开发程序的计算要求，采用四面体线性单元进行网格剖分。共 16122 个单元，3227 个节点。

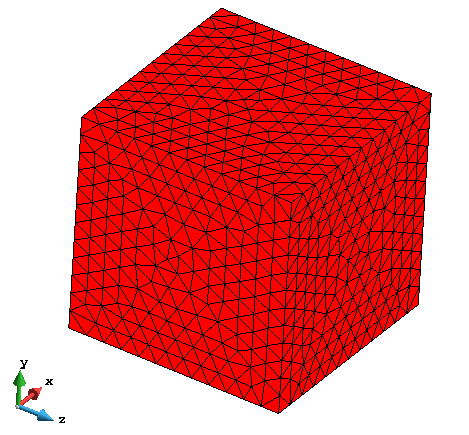
计算结果

本算例是有解析解的，具体形式为 $$u(x,y,z)=x+y+z$$ 观察计算结果可以看到，温度场的值从点 $(0,0,0)$ 的 $0\ { }^{\circ}\mathrm{C}$ 到点 $(1,1,1)$ 的 $3\ { }^{\circ}\mathrm{C}$ 的逐渐增大，呈线性分布。这与理论解完全一致，充分证明了算法和程序的有效性。