非线性 Poisson 方程

以一个简单的非线性 Poisson 方程为例，我们一起来看一下 FEtch 系统是如何求解非线性偏微分方程问题的。

问题描述

函数 $u(x,y)$ 满足如下非线性椭圆型方程：

\[-\nabla \cdot(\nabla u)=-16 \sqrt{u+1} \quad (\text { in } \Omega )\] \[u=0 \quad (\text { on } \partial \Omega)\]

其中，$\Omega$ 是位于坐标原点的一个单位圆盘， $\partial \Omega$ 是 $\Omega$ 的边界。该方程的精确解为 $u(x,y)=(x^2+y^2)^2-1$。求函数 $u(x,y)$ 的有限元解。

脚本文件

这是一个比较简单的单物理场问题。用有限元语言表述，只需要填写 4 种类型的文件，即 PDE、NFE、GCN 和 MDI 文件。

PDE 文件 (poisson.pde)，用于描述微分方程的弱形式。在有限元理论框架中，对应于单元矩阵的计算，是整个程序中最核心的部分。

defi
disp u
coor x y
shap %1 %2
gaus %3
coef un
mate ek 1.0

stif
\非线性系数修正,防止迭代计算崩溃
$c6 if (un < -1d0) then
$c6 	un = -1d0
$c6 endif
dist = +[u/x;u/x]*ek+[u/y;u/y]*ek

load = -[u]*16.0*dsqrt(un+1d0)

end

NFE 文件 (npsa.nfe)，与 PDE 文件相配合，用于给出待求解的矩阵格式的线性方程组（对应于整体矩阵组装）。同时还与 GCN 文件相配合，一起控制非线性迭代过程，并对计算结果作进一步处理。

defi
stif s
load f

coef u1

equation
vect u1,du
read(s,unod) u1,du
matrix = [s]
forc=[f]

solution u
vect ue
[ue]=[u]-[u1]
$c6 aa = 0.0
$c6 ab = 0.0
$c6 bb = 0.0
%nod
%dof
	aa = aa+[ue]*[ue]
	ab = ab+[ue]*[du]
	bb = bb+[du]*[du]
%dof
%nod
$c6 if (itn.eq.1 .or. cc.le.0) then
$c6   	cc = 1.0
$c6 else
$c6 	rab = sqrt(aa)*sqrt(bb)
$c6 	if (ab.gt.0.5*rab) cc = cc*2.0
$c6 	if (ab.gt.0.8*rab) cc = cc*2.0
$c6 	if (ab.lt.0.0) cc = cc*0.5
$c6 	if (ab.lt.-0.40*rab) cc = cc*0.5
$c6 	if (ab.lt.-0.80*rab) cc = cc*0.5
$c6 endif
$c6 if (cc.gt.1.0) cc = 1.0
$c6 err = aa
$c6 ul = 0.0
[u] = [u1]+[ue]*cc
%nod
%dof
	ul = ul + [u]*[u]
%dof
%nod
$c6 write(*,"('itn,cc,err=',i3,2e12.3)") itn,cc,err
$c6 if (err.lt.errb .or. err.lt.errb*ul .or. itn.ge.itnmax) then
$c6 	if (cc .ne. 1.0) then
$c6 		cc = -1
$c6 	else
$c6 		iend=1
gidpost("u",1.0) u(1)
[ue]=0.0
$c6 	endif
$c6 endif
write(s,unod) u,ue

end

GCN 文件 (nps.gcn)，用于定义求解器类型。同时与 NFE 文件相配合，一起组织计算流程。

defi
a nell

cc = 1.0
errb = 1.0e-8
itnmax = 100

#startsin a	
iend = 0
itn = 1
do while(iend==0)
	#solvsin a
	itn = itn+1
enddo

MDI 文件 (nps.mdi)，用于组织管理物理场信息。

2dxy
#a 1 1 u
pde poisson q4g2
#

实际操作中，这里的 NFE 文件可以调用系统的库文件自动生成，因此用户只需填写 PDE、GCN 和 MDI 三个文件即可，统计下来，总行数不超过 30 行！

我们通过 FEtch 客户端提交脚本文件后，会自动生成并下载有限元程序文件（nps.exe 和 run.bat）、材料参数文件（nps.mat）和 GiD 软件的前处理模板文件（nps.cnd 和 nps.bas）。编程任务至此已经顺利完成。

前处理

前处理和后处理都是通过第三方软件 GiD 来完成的。

我们首先进入 GiD 软件界面进行前处理。依次进行几何建模、施加边界条件、赋迭代初值、赋材料值和网格剖分，最终导出计算所需的数据输入文件（nps.dat)。

边界条件的施加情况如下

迭代初值的施加情况如下

使用的网格如下

计算结果

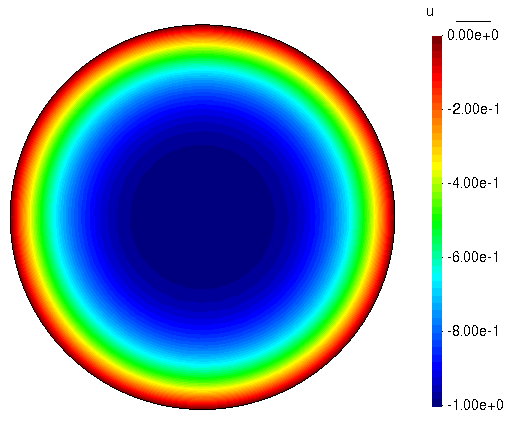
经过计算，总共使用了 50 次非线性迭代，生成了后处理文件（nps.flavia.res）。我们再次进入 GiD 软件界面进行后处理，查看云图效果如下。

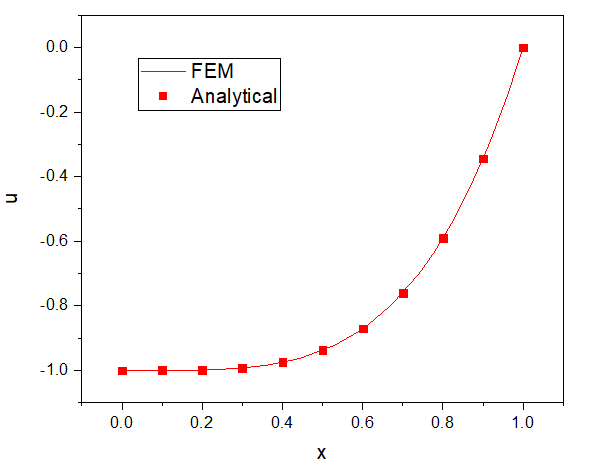
提取 x 轴上的计算结果并与解析解进行对比(如下图所示)，可以看出两者符合得很好。

至此，非线性 Poisson 方程的求解已顺利完成。

参考文献

[1]陆君安. 偏微分方程的MATLAB解法[J]. 武汉大学出版社, 2001.