稳态 Navier-Stokes 问题
关键词: 稳态 非线性 Navier-Stokes方程 Taylor-Hood单元
在流体力学领域,对于 Navier-Stokes 方程的混合有限元方法的研究一直是一个热点问题。通常的有限元法的求解困难在于:Navier-Stokes 方程要求有限元空间的组合必须满足 Ladyzhenskaya–Babuška–Brezzi(LBB)(或 inf–sup)相容性条件。正是这一条件的限制排除了传统的等阶插值有限元空间的使用。
求解 Navier-Stokes 方程使用最广泛的有限元族之一是 Taylor–Hood 族。 它由用于速度场的连续 $P_q (q \ge 2)$ 拉格朗日单元和用于压力场的连续 $P_{q−1}$ 拉格朗日单元组成。对于 $q = 2$,一维和二维的 Taylor–Hood 单元如下图所示。
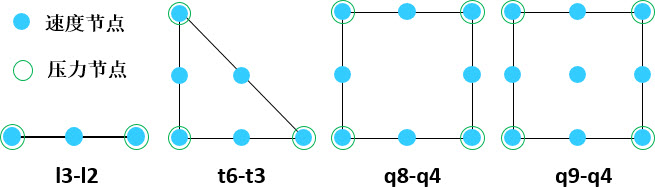
本节以二维稳态 Navier-Stokes 方程和 q9-q4 四边形单元为例,讲解如何使用 FEtch 系统提供的 Taylor–Hood 单元对流体力学问题进行全耦合求解。
控制方程
微分形式
Navier-Stokes 方程描述了流体运动。 对于域 $\Omega\subset\mathbb{R}^d\ (1\le d \le 3)$,稳态 Navier-Stokes 方程为:
\[\rho \left ( \boldsymbol{u}\cdot \nabla \right ) \boldsymbol{u} =- \nabla p+\mu\Delta \boldsymbol{u} + \rho \boldsymbol{f} \ \left(\text{in } \Omega\right) \tag{1a}\label{eq1}\] \[\nabla \cdot \boldsymbol{u} = 0 \ \left(\text{in } \Omega\right) \tag{1b}\]其中,$\boldsymbol{u}:\Omega \to \mathbb{R}^d$ 是速度场,$p:\Omega \to \mathbb{R}$ 是压力场,$\boldsymbol{f}:\Omega \to \mathbb{R}^d$ 是源项,$\rho$ 是流体密度, $\mu$ 是黏性系数。
这里仅考虑第一类边界条件,即在边界上给定速度和压力
\[\boldsymbol{u}=\bar{\boldsymbol{u}},\ p=\bar{p}\ \left(\text{on } \Gamma\right)\]弱形式
根据变分原理,稳态 Navier-Stokes 方程的弱形式如下
\[\int_{\Omega}\rho \left( ( \boldsymbol{u}\cdot \nabla ) \boldsymbol{u} \delta \boldsymbol{u}\right )d{\Omega}+\int_{\Omega}\mu \nabla \boldsymbol{u} \cdot \nabla \delta \boldsymbol{u} d{\Omega}-\int_{\Omega}p(\nabla \cdot \delta \boldsymbol{u}) d{\Omega}-\int_{\Omega}(\nabla \cdot \boldsymbol{u}) \delta p d{\Omega}=\int_{\Omega}\rho \boldsymbol{f} \cdot \delta \boldsymbol{u} d{\Omega}\]上式的第一项是非线性的,无法直接求解,需要引入迭代过程。最常用的处理方法是采用直接迭代法(也称 Picard 法)进行线性化,得到 \(\boldsymbol{u}^{n+1}\cdot\nabla \boldsymbol{u}^{n+1}\cong \boldsymbol{u}^n\cdot\nabla \boldsymbol{u}^{n+1}\) 其中,上标 $n$ 表示迭代步数。这样,稳态 Navier-Stokes 方程的弱形式可以进一步表示为 \(\int_{\Omega}\rho \left( ( \boldsymbol{u}^n\cdot \nabla ) \boldsymbol{u}^{n+1} \delta \boldsymbol{u}^{n+1}\right )d{\Omega}+\int_{\Omega}\mu \nabla \boldsymbol{u}^{n+1} \cdot \nabla \delta \boldsymbol{u}^{n+1} d{\Omega}-\int_{\Omega}p^{n+1}(\nabla \cdot \delta \boldsymbol{u}^{n+1}) d{\Omega}\\-\int_{\Omega}(\nabla \cdot \boldsymbol{u}^{n+1}) \delta p^{n+1} d{\Omega}=\int_{\Omega}\rho \boldsymbol{f} \cdot \delta \boldsymbol{u}^{n+1} d{\Omega}\) 在二维直角坐标系下,令 $\boldsymbol{u}=(u,v)$,$\boldsymbol{f}=(f_x,f_y)$,上式可写成 \(\begin{align} & \int_{\Omega}\rho (u^n \frac{\partial u^{n+1}}{\partial x}+v^n \frac{\partial u^{n+1}}{\partial y}) \delta u^{n+1}+ \rho(u^n \frac{\partial v^{n+1}}{\partial x}+v^n \frac{\partial v^{n+1}}{\partial y}) \delta v^{n+1}d{\Omega} \\ &-\int_{\Omega}{\left (p^{n+1}(\frac{\partial \delta u^{n+1}}{\partial x}+\frac{\partial \delta v^{n+1}}{\partial y})+(\frac{\partial u^{n+1}}{\partial x}+\frac{\partial v^{n+1}}{\partial y})\delta p^{n+1}\right)d{\Omega}} \\ & +\int_{\Omega}{\mu (\frac{\partial u^{n+1}}{\partial x}\frac{\partial \delta u^{n+1}}{\partial x}+\frac{\partial u^{n+1}}{\partial y}\frac{\partial \delta u^{n+1}}{\partial y}+\frac{\partial v^{n+1}}{\partial x}\frac{\partial \delta v^{n+1}}{\partial x}+\frac{\partial v^{n+1}}{\partial y}\frac{\partial \delta v^{n+1}}{\partial y})d{\Omega}}\\ &=\int_{\Omega}{\rho ({f_{x}}\delta u^{n+1}+{f_{y}}\delta v^{n+1})d{\Omega}} \\ \end{align} \tag{2}\label{eq2}\)
脚本编写
一个具体问题的有限元语言表述,通常需要包含 5 种类型的文件:PDE、FBC、MDI、GCN 和 NFE。由于方程 $\eqref{eq2}$ 不存在边界积分项,所以这里不需要写 FBC 文件。下面依次给出其他 4 个文件的详细介绍。
PDE 文件
在这个例子中,采用全耦合的方法,将流速和压力视为同一个物理场。根据有限元语言的语法规则,将方程 $\eqref{eq2}$ 的体积分项写入 PDE 文件如下。
| diffconv.pde | 说明 |
|---|---|
| defi disp u,v,p coor x,y shap %1 %2 shap %1 4 p gaus %3 func div,cu,cv coef un,vn mate rou emu fx fy 1.0 1d-3 0.0 0.0 func div=+[u/x]+[v/y] cu=+[u/x]*un+[u/y]*vn cv=+[v/x]*un+[v/y]*vn stif dist= +[u/x;u/x]*emu+[u/y;u/y]*emu +[v/x;v/x]*emu+[v/y;v/y]*emu +[cu;u]*rou+[cv;v]*rou -[p;div]-[div;p] load=+[u]*fx*rou+[v]*fy*rou end |
系统关键字(信息定义) 定义未知量 定义坐标分量 定义采用的形函数 特别定义 p 变量的形函数由 4 个节点插值 定义采用的积分方式 声明自定义函数 定义非线性变量,引入上一迭代步的流速值 定义用到的材料参数和默认参数值 (空行) 系统关键字(向量函数表达式) 自定义函数的具体表达式 (空行) 系统关键字(单元刚度矩阵表达式定义) 刚度矩阵项,对应式 $\eqref{eq2}$ 左侧 (空行) 荷载向量项,对应式 $\eqref{eq2}$ 右侧 (空行) 系统关键字(文件结束) |
这里将 shap 行和 gaus 行的参数设为待定,参数值 %1、%2 和 %3 将从 MDI 文件中取得。
注意,脚本文本中存在两个 shap 行。多出来的第二个 shap 行是 Taylor-Hood 单元所特有的,用于对未知量 p 的形函数进行特别定义,指定其为 4 节点的线性插值。
MDI 文件
MDI 文件负责组织 PDE 和 FBC 文件,声明程序具体使用的坐标系统、单元类型和积分方法。这里文件命名为 ns.mdi,具体内容如下。
| ns.mdi | 说明 |
|---|---|
| 2dxy #a 0 3 u v p_ pde diffconv q9g3 # |
在二维直角坐标系下求解 a 场,无初值,3 个自由度,名称为 u v p,p 采用低阶插值 调用 diffconv.pde,采用 9 节点四边形单元,3 点高斯积分 (文件结束符,可留空) |
特别注意,自由度 p 的右侧加了下划线 “_”,代表它采用的形函数的阶次要比当前的单元阶次低一阶。同时,下划线 “_” 的使用一定要和 PDE 文件中的 shap 行匹配好,否则会出现致命错误。
MDI 文件声明的单元类型和积分方式将以参数的形式传递给 PDE 文件中的的 %1、%2 和 %3。如果后续想要使用其他的单元类型或者积分方法,只需修改 MDI 文件即可。
GCN 文件
GCN 文件给出计算流程信息,系统规定其文件名字要与 MDI 文件一致。作为非线性稳态问题,本算例的计算流程并不复杂,只需填写少量代码,具体内容如下。
| ns.gcn | 说明 |
|---|---|
| defi a nell errb = 1.0e-8 itnmax = 50 #startumf a iend = 0 itn = 1 do while(iend==0) #solvumf a itn = itn+1 enddo |
算法引入段 a 场,采用的算法模板文件为 nell.nfe (空行) 开始命令流段 收敛阈值 迭代次数上限 初始化 a 场,使用 umf 求解器 对迭代标记 iend 赋初值,iend 是系统保留字,整数型全局变量 对迭代次数 itn 赋初值,itn 是系统保留字,整数型全局变量 迭代循环开始 求解 a 场,计算过程中 a 场会更新 iend 的值 迭代次数更新 迭代循环结束 |
注意,这里推荐使用 umf 求解器,它可以很好地保证计算的稳定性和精度。如果采用 sin 求解器,由于存在压力项矩阵的对角位置为零的情况,计算通常是不收敛的。此时需要对控制方程添加稳定项,进而需要改写 PDE 文件。感兴趣的高级用户可自行尝试实现。
NFE 文件
GCN 文件使用了 nell 算法,系统会基于模板文件自动生成以下的 nsa.nfe 文件。这里需要修改的是 gidpost 输出语句:
- 速度(矢量)和压力(标量)在物理本质上是两个场,在将结果保存到 GiD 后处理文件时需要进行区分,即采用两次 gidpost 语句,分开输出。
修改完成后的文件内容如下。
| nsa.nfe | 说明 |
|---|---|
| defi stif s load f coef u1 equation vect u1,du read(s,unod) u1,du matrix = [s] forc=[f] solution u vect ue [ue]=[u]-[u1] $c6 aa = 0.0 $c6 ab = 0.0 $c6 bb = 0.0 %nod %dof aa = aa+[ue]*[ue] ab = ab+[ue]*[du] bb = bb+[du]*[du] %dof %nod $c6 if (itn.eq.1 .or. cc.le.0) then $c6 cc = 1.0 $c6 else $c6 factor=2.0 $c6 rab = sqrt(aa)*sqrt(bb) $c6 if (ab.gt.0.5*rab) cc = cc*factor $c6 if (ab.gt.0.8*rab) cc = cc*factor $c6 if (ab.lt.0.0) cc = cc/factor $c6 if (ab.lt.-0.40*rab) cc = cc/factor $c6 if (ab.lt.-0.80*rab) cc = cc/factor $c6 endif $c6 if (cc.gt.1.0) cc = 1.0 $c6 if (cc.lt.-1.0) cc = -1.0 [u] = [u1]+[ue]*cc $c6 err = aa $c6 ul = 0.0 %nod %dof ul = ul + [u]*[u] %dof %nod $c6 write(*,"('itn,cc,err=',i3,2e12.3)") itn,cc,err $c6 if (err.lt.errb .or. err.lt.errb*ul .or. itn.ge.itnmax) then $c6 if (cc .ne. 1.0) then $c6 cc = -1 $c6 else $c6 iend=1 gidpost("u v",1.0) u(1),u(2) gidpost("p",1.0) u(3) [ue]=0.0 $c6 endif $c6 endif write(s,unod) u,ue end |
DEFI段 定义刚度矩阵名为 s 定义载荷向量名为 f (空行) 耦合的场向量 (空行) EQUATION段 定义场向量 读入上一迭代步的结果 方程组左端矩阵 方程组右端向量 (空行) SOLUTION段 定义求解的场向量 计算当前迭代步增量 ue 循环所有节点上的所有自由度 计算 ue 的模的平方和 aa 计算 ue 与 du 的广义内积 ab 计算 du 的模的平方和 bb 依据当前迭代步增量 ue与 上一迭代步增量 du 之间的夹角, 来调整松弛因子 当夹角为锐角时,适当放大 cc 当夹角为钝角时,则适当缩小 cc 用松弛因子调整计算结果 收敛判断 记录迭代收敛情况 继续迭代标记,保证收敛时的 cc = 1 迭代结束标志更新 将速度结果写入 GiD 后处理文件 将压力结果写入 GiD 后处理文件 临时存储当前的结果,供下一迭代步读取 (空行) 结束标记 |
算例1
泊肃叶流动
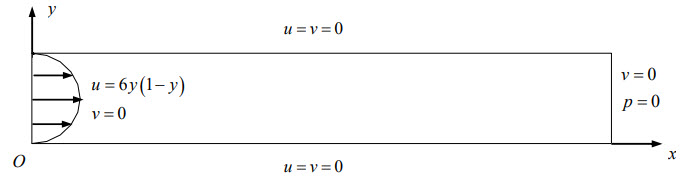
平面泊肃叶流(Poiseuille flow)是少数存在理论解的流动问题之一,其几何模型及边界条件如下图所示。计算模型中 $y$ 方向取特征长度 $L = 1\ \mathrm{m}$,腔体长高比取 $6:1$,液体密度 $\rho= 1.0\ \mathrm{kg/m^3}$,黏性系数 $\mu = 0.01\ \mathrm{Pa\cdot s}$。 入口处的无因次速度按抛物线分布为 $u = 6y(1-y)$,$v = 0$,固壁面上满足不可滑移条件 $u = 0$ ,$v = 0$,出口处压力 $p = 0$。
平面泊肃叶流的压力理论解为 \(p = 12\mu(6-x)\)
前处理
填写材料参数文件
系统自动生成了 ns.mat 文件,用于设置材料参数。对于当前算例,文件具体内容如下。
| ns.mat | 说明 |
|---|---|
| 1 5 aeq9g3 num rou emu fx fy 1 1.0 1d-2 0.0 0.0 # |
9 节点四边形面单元 材料参数 参数值 分隔符 |
赋单元材料
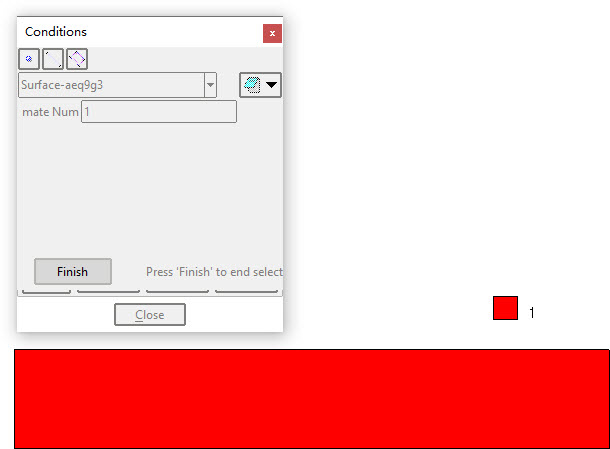
施加第一类边界条件
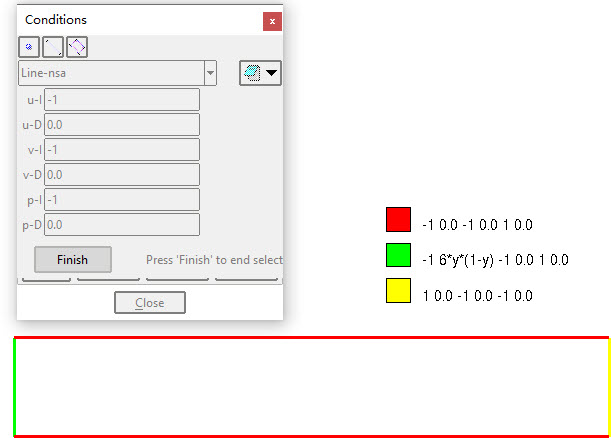
其中:
u-I 为边界类型,-1 表示约束,1 表示自由
u-D 为相应的约束值或施加节点力
由于有不同的边界条件交接,角点位置上的边界条件可能出现歧义。为此,继续明确定义角点处的边界条件。
网格剖分
网格剖分采用 9 节点四边形单元,共使用了 600 个单元,2541 个节点。

计算结果
水平流速分量的分布
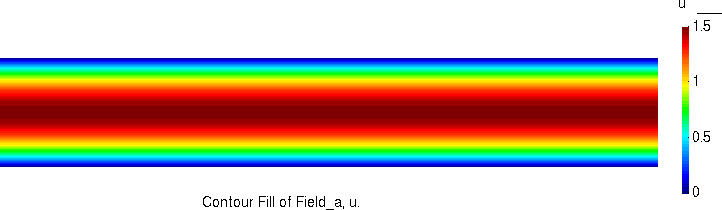
竖直流速分量的分布

压力的分布

可以看出,计算结果与解析解符合得很好,充分证明的了算法和程序的正确性。
算例2
顶盖驱动方腔流
顶盖驱动方腔流(Lid-driven Cavity Flow)是验证流体动力学问题计算方法的一个基准案例。考虑一个二维的 $1\ \mathrm{m}×1\ \mathrm{m}$ 的方腔,内部流体的初始速度和压力都是零,现在顶部一无限长的滑板以 $1 \mathrm{m/s}$ 的速度向右拖动顶部流体,求稳定后方腔内部的流场速度和压力的分布情况。
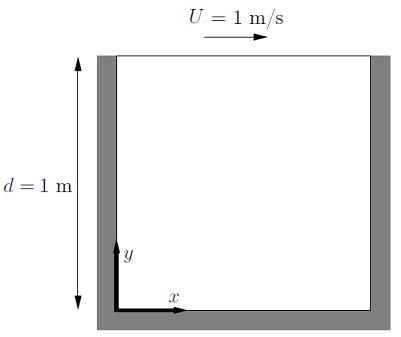
设流体的密度 $\rho =1.0\ \mathrm{kg/m^3}$,黏性系数 $\mu =1.0\times 10^{-3}\ \mathrm{Pa\cdot s}$,体积力 $f =0.0$。
边界条件为:上面边界上的流体速度 $u=1.0$,$v=0$。其他三边上都为固壁边界条件 $u=0$,$v=0$。在 $(0,0,0)$ 点处给定参考压力 $p=0$。
前处理
填写材料参数文件
系统自动生成了 ns.mat 文件,用于设置材料参数。参数初始值全部为 PDE 文件给出的默认值。文件具体内容如下。
| ns.mat | 说明 |
|---|---|
| 1 5 aeq9g3 num rou emu fx fy 1 1.0 1d-3 0.0 0.0 # |
9 节点四边形面单元 材料参数 参数值 分隔符 |
赋单元材料
施加第一类边界条件
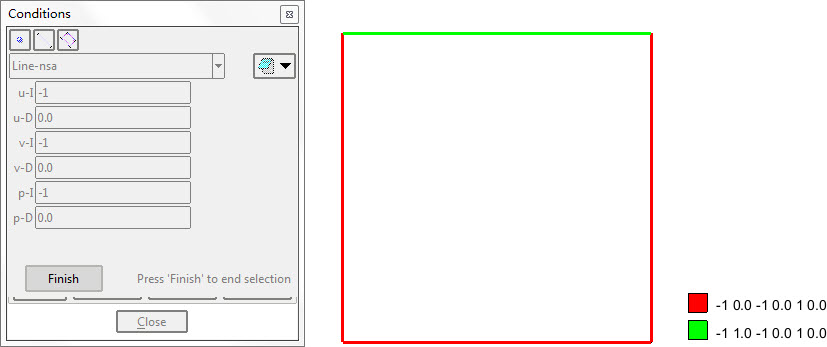
其中:
u-I 为边界类型,-1 表示约束,1 表示自由
u-D 为相应的约束值或施加节点力
由于有不同的边界条件交接,角点位置上的边界条件可能出现歧义。为此,继续明确定义角点处的边界条件。
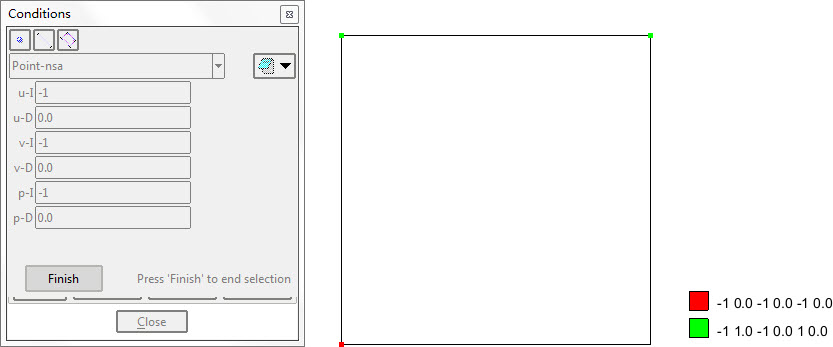
网格剖分
根据所开发程序的计算要求,网格剖分采用 9 节点四边形单元,并对边界位置进行了局部加密。共使用了 2500 个单元,10201 个节点。

计算结果
水平流速分量的分布
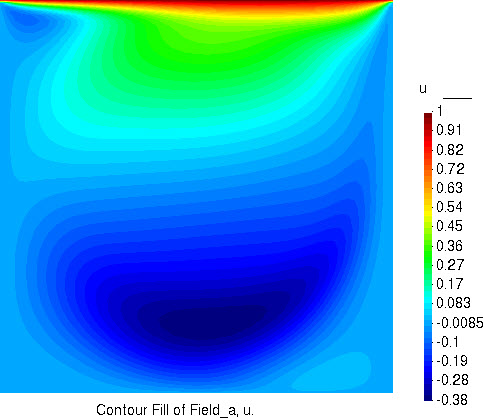
竖直流速分量的分布
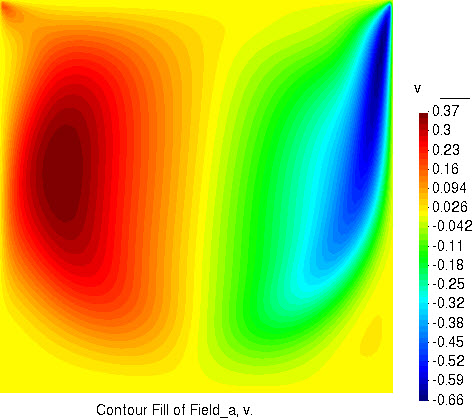
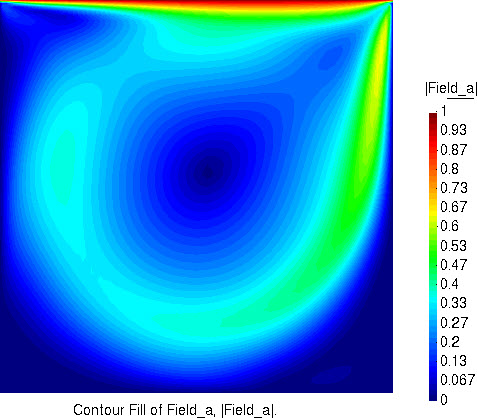
流速大小的分布
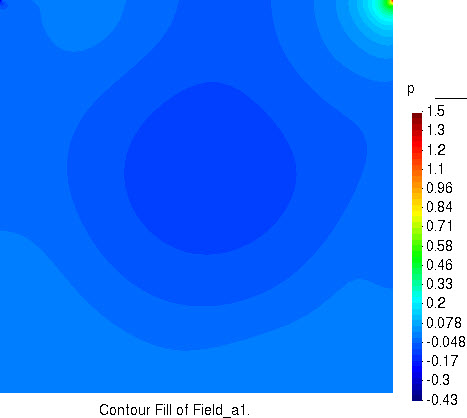
压力的分布
深入讨论
上面的算例对应的雷诺数为 $Re=1000$ 。通过调整黏性系数 $\mu$,重新计算,可以得到 $Re=100$ 和 $Re=5000$ 时的数据结果。
速度沿中线的分布
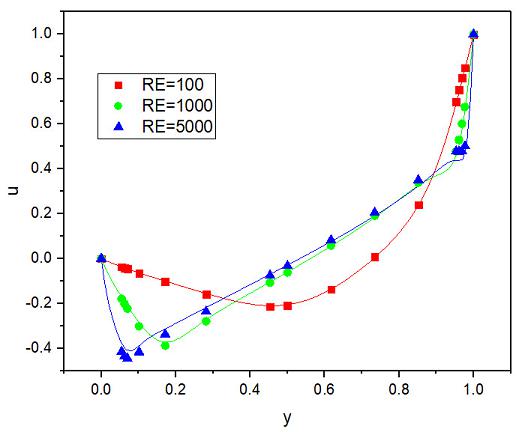
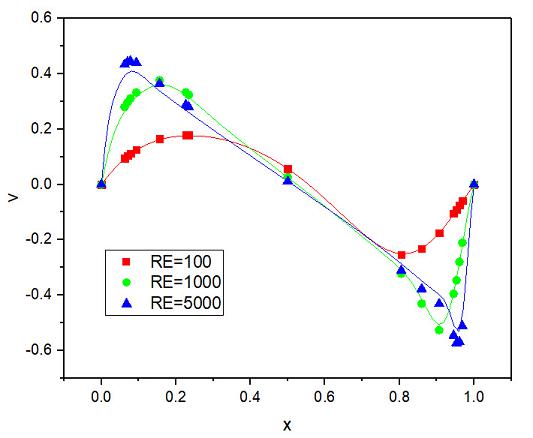
上图给出了不同雷诺数下水平速度 $u$ 沿垂直中线、竖直速度 $v$ 沿水平中线的分布结果。图中实线表示 FEtch 生成程序的计算结果;点表示 Tamer 等(2017)1 采用有限体积法的计算结果,其结果被视为标准解。由图可见本程序的计算结果与 Tamer 等的计算结果十分吻合。
我们还注意到,随着雷诺数的增大,解的光滑性降低,在边界位置的计算结果的误差略有上升。这与网格密度大小直接相关。如果进一步加密网格进行计算分析,可以进一步提高计算精度,逼近真解。在 Tamer 等的模型中,网格节点数为 $1031\times1031$,而这里采用的网格节点仅为 $101\times101$,远少于 Tamer 等模型中采用的节点数。 以上分析表明,即使在较少网格的情况下,我们这里采用的有限元算法也能达到较高的精度。
非线性迭代次数统计
| 雷诺数 $Re$ | 100 | 1000 | 5000 |
|---|---|---|---|
| 迭代次数 | 8 | 16 | 28 |
上表统计了不同雷诺数时计算使用的迭代次数。随着雷诺数增大,问题的非线性增强,相应迭代次数也有所上升,但数目仍在可接受范围之内。当 $Re=5000$ 时,迭代次数也仅仅用了 28 次,充分说明了这里采用的迭代算法能够很好地保证收敛性和计算效率。
参考文献
-
Tamer A. AbdelMigid, Khalid M. Saqr, et al. Revisiting the lid-driven cavity flow problem: Review and new steady state benchmarking results using GPU accelerated code. Alexandria Engineering Journal, 2017. ↩





