瞬态 Navier-Stokes 问题
关键词: 瞬态 非线性 算子分裂 Navier-Stokes方程 Taylor-Hood单元
在流体力学领域,对于 Navier-Stokes 方程的混合有限元方法的研究一直是一个热点问题。通常的有限元法的求解困难在于:Navier-Stokes 方程要求有限元空间的组合必须满足 Ladyzhenskaya–Babuška–Brezzi(LBB)(或 inf–sup)相容性条件。正是这一条件的限制排除了传统的等阶插值有限元空间的使用。
求解 Navier-Stokes 方程使用最广泛的有限元族之一是 Taylor–Hood 族。 本节以二维瞬态 Navier-Stokes 方程和 q9-q4 四边形单元为例,讲解如何使用 FEtch 系统提供的 Taylor–Hood 单元,结合算子分裂法,对瞬态流体力学问题进行耦合求解。
控制方程
微分形式
Navier-Stokes 方程描述了流体运动。 对于域 $\Omega\subset\mathbb{R}^d\ (1\le d \le 3)$,瞬态 Navier-Stokes 方程为:
\[\rho \frac{\partial \boldsymbol{u}}{\partial t} +\rho \left ( \boldsymbol{u}\cdot \nabla \right ) \boldsymbol{u} =- \nabla p+\mu\Delta \boldsymbol{u} + \rho \boldsymbol{f} \quad \left(\text{ in } \Omega\right)\\ \nabla \cdot \boldsymbol{u} = 0 \qquad \left(\text{ in } \Omega\right)\]其中,$\boldsymbol{u}:\Omega \to \mathbb{R}^d$ 是速度场,$p:\Omega \to \mathbb{R}$ 是压力场,$\boldsymbol{f}:\Omega \to \mathbb{R}^d$ 是源项,$\rho$ 是流体密度, $\mu$ 是黏性系数。
这里仅考虑第一类边界条件,即在边界上给定速度和压力
\[\boldsymbol{u}=\bar{\boldsymbol{u}},\quad p=\bar{p}\quad\left(\text{ on } \Gamma\right)\]我们采用算子分裂算法,把N-S 方程描述的物理过程分解为扩散和对流两个过程,分别计算。这样可以避免两个不同性质的物理过程一起求解时,在计算上带来的困难。
扩散方程为
\[\rho \frac{\partial \boldsymbol{u}}{\partial t}=- \nabla p+\mu\Delta \boldsymbol{u} + \rho \boldsymbol{f} \\ \nabla\cdot \boldsymbol{u}=0 \tag{1}\label{eq1}\]对流方程为
\[\rho \frac{\partial \boldsymbol{u}}{\partial t} +\rho \left ( \boldsymbol{u}\cdot \nabla \right ) \boldsymbol{u} =0 \tag{2}\label{eq2}\]弱形式
扩散方程
根据变分原理,方程 $\eqref{eq1}$ 的的弱形式为
\[\int_{\Omega}{\rho (}\frac{\partial \boldsymbol{u}}{\partial t}\delta \boldsymbol{u})d{\Omega}+\int_{\Omega}\mu \nabla \boldsymbol{u} \cdot \nabla \delta \boldsymbol{u} d{\Omega}\\-\int_{\Omega}p(\nabla \cdot \delta \boldsymbol{u}) d{\Omega}-\int_{\Omega}(\nabla \cdot \boldsymbol{u}) \delta p d{\Omega}=\int_{\Omega}\rho \boldsymbol{f} \cdot \delta u d{\Omega}\]在二维直角坐标系下,令 $\boldsymbol{u}=(u,v)$,$\boldsymbol{f}=(f_x,f_y)$,上式可写成
\[\int_{\Omega}{\rho (}\frac{\partial u}{\partial t}\delta u+\frac{\partial v}{\partial t}\delta v)d{\Omega}+\int_{\Omega}{\mu \left (\frac{\partial u}{\partial x}\frac{\partial \delta u}{\partial x}+\frac{\partial u}{\partial y}\frac{\partial \delta u}{\partial y}+\frac{\partial v}{\partial x}\frac{\partial \delta v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial \delta v}{\partial y}\right)d{\Omega}}\\-\int_{\Omega}{\left (p(\frac{\partial \delta u}{\partial x}+\frac{\partial \delta v}{\partial y})+(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y})\delta p\right)d{\Omega}}=\int_{\Omega}{\rho \left(f_{x}\delta u+f_{y}\delta v\right)d{\Omega}} \tag{3}\label{eq3}\]注意到这是一个瞬态方程,后面我们采用标准的向后差分法,继续进行时域离散,即可顺利求解。
对流方程
我们采用 CBS(基于算子分裂的特征线)方法来求解对流方程,利用基于特征线的显式时间离散法将对流项线性化,由方程 $\eqref{eq2}$ 得到
\[\boldsymbol{u}^{n+1}=\boldsymbol{u}^n-\Delta t \boldsymbol{u}^n\cdot\nabla \boldsymbol{u}^n+\frac{\Delta t^2}{2}(\boldsymbol{u}^n\cdot\nabla)(\boldsymbol{u}^n\cdot\nabla \boldsymbol{u}^n)\]其中,上标 $n$ 表示时间步数,$\Delta t$ 为时间步长。上式最后一项可以理解为直接由对流方程推导出来的沿流线的稳定扩散项。这样,对流方程的弱形式可以表示为
\[\int_{\Omega}\boldsymbol{u}^{n+1}\delta \boldsymbol{u}^{n+1}d{\Omega}=\int_{\Omega}\boldsymbol{u}^n\delta \boldsymbol{u}^{n+1}d{\Omega}-\int_{\Omega}\Delta t (\boldsymbol{u}^n\cdot\nabla \boldsymbol{u}^n)\delta \boldsymbol{u}^{n+1}d{\Omega} \\ -\int_{\Omega}\frac{\Delta t^2}{2}(\boldsymbol{u}^n\cdot\nabla \boldsymbol{u}^n)(\boldsymbol{u}^n\cdot\nabla \delta \boldsymbol{u}^{n+1} ) d{\Omega}\]在二维直角坐标系下,上式可写成
\[\begin{align} & \int_{\Omega}(u^{n+1}\delta u^{n+1}+v^{n+1}\delta v^{n+1})d{\Omega}= \int_{\Omega}(u^n\delta u^{n+1}+v^n\delta v^{n+1})d{\Omega}\\ & -\Delta t\int_{\Omega}(u^n \frac{\partial u^n}{\partial x}+v^n \frac{\partial u^n}{\partial y}) \delta u^{n+1}d{\Omega}-\Delta t\int_{\Omega} (u^n \frac{\partial v^n}{\partial x}+v^n \frac{\partial v^n}{\partial y}) \delta v^{n+1}d{\Omega} \\ & -\frac{\Delta t^2}{2}\int_{\Omega}(u^n \frac{\partial u^n}{\partial x}+v^n \frac{\partial u^n}{\partial y}) (u^n \frac{\partial \delta u^{n+1}}{\partial x}+v^n \frac{\partial \delta u^{n+1}}{\partial y})d{\Omega}\\ & -\frac{\Delta t^2}{2}\int_{\Omega} (u^n \frac{\partial v^n}{\partial x}+v^n \frac{\partial v^n}{\partial y}) (u^n \frac{\partial \delta v^{n+1}}{\partial x}+v^n \frac{\partial \delta v^{n+1}}{\partial y})d{\Omega} \end{align} \tag{4}\label{eq4}\]上式本质上是一种显式算法,因此时间步长的选择有一定的限制。试算实验1指出,为了实现较高的计算精度,时间步长的选取应满足正比于 $Re^{-3/4}$。
脚本编写
一个具体问题的有限元语言表述,通常需要包含 5 种类型的文件:PDE、FBC、MDI、GCN 和 NFE。由于方程 $\eqref{eq3}$ 和 $\eqref{eq4}$ 都不存在边界积分项,所以这里不需要写 FBC 文件。下面依次给出其他 4 个文件的详细介绍。
PDE 文件
扩散方程
求解扩散方程时,采用全耦合的方法,将流速和压力视为同一个物理场。根据有限元语言的语法规则,将方程 $\eqref{eq3}$ 的体积分项写入 PDE 文件如下。
| diff.pde | 说明 |
|---|---|
| defi disp u v p coor x y shap %1 %2 shap %1 4 p gaus %3 func div mass %1 rou rou 0.0 mate rou emu fx fy 1.0 1d-3 0.0 0.0 func div=+[u/x]+[v/y] stif dist=+[u/x;u/x]*emu+[u/y;u/y]*emu +[v/x;v/x]*emu+[v/y;v/y]*emu -[div;p]-[p;div] load=+[u]*rou*fx+[v]*rou*fy end |
系统关键字(信息定义) 定义未知量 定义坐标分量 定义采用的形函数 特别定义 p 变量的形函数由 4 个节点插值 定义采用的积分方式 声明自定义函数 定义集中质量矩阵,对应式 $\eqref{eq3}$ 左侧第 1 项 定义用到的材料参数和默认参数值 (空行) 系统关键字(向量函数表达式) 自定义函数的具体表达式 (空行) 系统关键字(单元刚度矩阵表达式定义) 刚度矩阵项,对应式 $\eqref{eq3}$ 左侧第 2、3 项 (空行) 荷载向量项,对应式 $\eqref{eq3}$ 右侧 (空行) 系统关键字(文件结束) |
这里将 shap 、gaus 和 mass 行的参数设为待定,参数值 %1、%2 和 %3 将从 MDI 文件中取得。
注意,脚本文本中存在两个 shap 行。多出来的第二个 shap 行是 Taylor-Hood 单元所特有的,用于对未知量 p 的形函数进行特别定义,指定其为 4 节点的线性插值。
对流方程
对流方程对应式 $\eqref{eq4}$,利用有限元语言语法编写的 PDE 文件如下
| conv.pde | 说明 |
|---|---|
| defi disp u v coor x y coef un vn shap %1 %2 gaus %3 func lu lv mass %1 1.0 mate rou emu fx fy 1d3 1d-3 0 0 func $cv fu = +{un/x}*un+{un/y}*vn $cv fv = +{vn/x}*un+{vn/y}*vn lu=+[u/x]*un+[u/y]*vn lv=+[v/x]*un+[v/y]*vn stif null load=+[u]*un+[v]*vn -[u]*fu*dt-[v]*fv*dt -[lu]*fu*dt*dt/2-[lv]*fv*dt*dt/2 end |
系统段落关键字(信息定义) 定义未知量 定义坐标分量 声明耦合变量,引入扩散方程求得的流速值 定义采用的形函数 定义采用的积分方式 声明自定义函数 定义集中质量矩阵,对应式 $\eqref{eq4}$ 左侧第 1 项 定义用到的材料参数和参数值 (空行) 系统关键字(向量函数表达式) 自定义函数的具体表达式 (空行) 系统段落关键字(单元刚度矩阵表达式定义) 单元刚度矩阵为零矩阵 (空行) 荷载向量项,对应式 $\eqref{eq4}$ 右侧 (空行) 系统关键字(文件结束) |
MDI 文件
MDI 文件负责组织 PDE 和 FBC 文件,声明程序具体使用的坐标系统、单元类型和积分方法。这里文件命名为 ns.mdi,具体内容如下。
| ns.mdi | 说明 |
|---|---|
| 2dxy #a 1 3 u v p_ pde diff q9 #b 0 2 u v pde conv q9 # |
在二维直角坐标系下求解 a 场,1 个初值,3 个自由度,名称为 u v p,p 采用低阶插值 调用 diff.pde,采用 9 节点四边形单元,节点积分 b 场,无初值,2 个自由度,名称为 u v 调用 conv.pde,采用 9 节点四边形单元,节点积分 (文件结束符,可留空) |
特别注意,自由度 p 的右侧加了下划线 “_”,代表它采用的形函数的阶次要比当前的单元阶次低一阶。同时,下划线 “_” 的使用一定要和 PDE 文件中的 shap 行匹配好,否则会出现致命错误。
MDI 文件声明的单元类型和积分方式将以参数的形式传递给 PDE 文件中的的 %1、%2 和 %3。如果后续想要使用其他的单元类型或者积分方法,只需修改 MDI 文件即可。
GCN 文件
GCN 文件给出计算流程信息,系统规定其文件名字要与 MDI 文件一致。采用算子分裂法后,原来的非线性问题转化为了交错耦合的线性瞬态问题。本算例的计算流程并不复杂,主要思路是在时间循环体内部依次求解 a 场和 b 场,具体内容如下。
| ns.gcn | 说明 |
|---|---|
| defi a parb b str a open(21,file='time.dat',form='formatted') read(21,*) dt,tmax close(21) #startumf a time = dt do while (time <= tmax+1e-8) #solvumf a #stress b a time = time + dt enddo |
算法引入段 a 场,采用的算法模板文件为 nell.nfe b 场,采用算法模板文件为 str.nfe,耦合 a 场 (空行) 开始命令流段 从 time.dat 文件读取时间步参数 初始化 a 场,使用 umf 求解器 给 time 赋初始值 迭代循环开始 求解 a 场 求解 b 场,直接用 a 场的输入数据 更新 time 迭代循环结束 |
注意,这里推荐使用 umf 求解器,它可以很好地保证计算的稳定性和精度。如果采用 sin 求解器,由于存在压力项矩阵的对角位置为零的情况,计算通常是不收敛的。此时需要对控制方程添加稳定项,进而需要改写 PDE 文件。感兴趣的高级用户可自行尝试实现。
NFE 文件
扩散方程
GCN 文件使用了 parb 算法,系统会基于模板文件自动生成以下的 nsa.nfe 文件。由于 a 场计算得到的速度结果还会由 b 场继续读取并更新,只有压力结果是计算完成的,因此,这里修改了 gidpost 输出语句,仅将压力结果写入 GiD 后处理文件。同时,为了减少输出次数,我们还添加了判读语句,每 10 个时间步输出 1次计算结果。修改完成后的文件内容如下。
| nsa.nfe | 说明 |
|---|---|
| defi stif s mass m load f equation vect u read(s,unod) u matrix = [s]*dt+[m] forc = [f]*dt+[m]*[u] solution u write(s,unod) u $c6 if(mod(nint(time/dt),10).eq. 0) then gidpost("p",time) u(3) $c6 endif end |
DEFI段 定义刚度矩阵名为 s 定义质量矩阵名为 m 定义载荷向量名为 f (空行) EQUATION段 定义场向量 读入上一时间步的场向量值 方程组左端矩阵 方程组右端向量 (空行) SOLUTION段 定义求解的场向量 临时存储当前的结果,供 b 场读取 每 10 个时间步 1次 将压力结果写入 GiD 后处理文件 (空行) 结束标记 |
对流方程
利用扩散方程的计算结果,对流方程使用了 str 算法,系统会基于模板文件自动生成以下的 nsb.nfe 文件。这里同样修改了 gidpost 输出语句,每 10 个时间步输出 1 次速度结果。
| nsb.nfe | 说明 |
|---|---|
| defi stif s mass m load f coef u v equation var u v p read(s,unod) u v p matrix = [m] forc = [f] solution uv $c6 if(mod(nint(time/dt),10) .eq. 0) then gidpost("u v",time) uv(1),uv(2) $c6 endif write(s,unod) uv,p end |
DEFI段 定义刚度矩阵名为 s 定义质量矩阵名为 m 定义载荷向量名为 f (空行) coef 语句 声明耦合变量 (空行) EQUATION段 定义耦合变量 从 a 场保存的 unod 文件读取耦合变量 u v p 方程组左端矩阵为质量矩阵 方程组右端向量为载荷向量 (空行) SOLUTION段 定义求解的场向量 每 10 个时间步 1次 将速度结果写入 GiD 后处理文件 临时存储当前的结果,供 a 场读取 (空行) 结束标记 |
注意,NFE 文件的 coef 行,要保证与 PDE文件中 coef 行耦合场变量的数目和顺序保持一致,否则会出现信息传递错误。
算例
顶盖驱动方腔流
顶盖驱动方腔流(Lid-driven Cavity Flow)是验证流体动力学问题计算方法的一个基准案例。考虑一个二维的 $1\ \mathrm{m}×1\ \mathrm{m}$ 的方腔,内部流体的初始速度和压力都是零,现在顶部一无限长的滑板以 $1 \mathrm{m/s}$ 的速度向右拖动顶部流体,求方腔内部的流场速度和压力的演化过程。
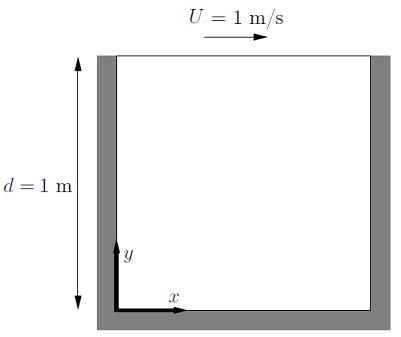
设流体的密度 $\rho =1.0\ \mathrm{kg/m^3}$,黏性系数 $\mu =1.0\times 10^{-3}\ \mathrm{Pa\cdot s}$,体积力 $f =0.0$。
边界条件为:上面边界上的流体速度 $u=1.0$,$v=0$。其他三边上都为固壁边界条件 $u=0$,$v=0$。在 $(0,0,0)$ 点处给定参考压力 $p=0$。
前处理
填写材料参数文件
系统自动生成了 ns.mat 文件,用于设置材料参数。参数初始值全部为 PDE 文件给出的默认值。文件具体内容如下。注意,由于 b 场的计算直接使用了 a 场的网格数据作为输入数据,所以 MAT 文件中没有与 b 场相关的单元和参数选项。
| ns.mat | 说明 |
|---|---|
| 1 5 aeq9 num rou emu fx fy 1 1.0 1d-3 0.0 0.0 # |
9 节点四边形面单元 材料参数 参数值 分隔符 |
填写时间步长文件
由 ns.gcn 文件可知,用户自定义了时间步长文件 time.dat,给出时间步长和终止时间。文件内容如下:
0.01 30
由此可知,时间步长为 0.01 s,计算终止时间为 30 s。
赋单元材料
施加第一类边界条件
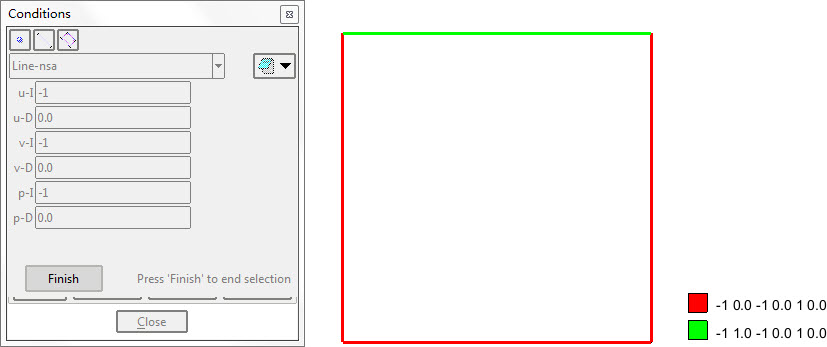
其中:
u-I 为边界类型,-1 表示约束,1 表示自由
u-D 为相应的约束值或施加节点力
由于有不同的边界条件交接,角点位置上的边界条件可能出现歧义。为此,继续明确定义角点处的边界条件。
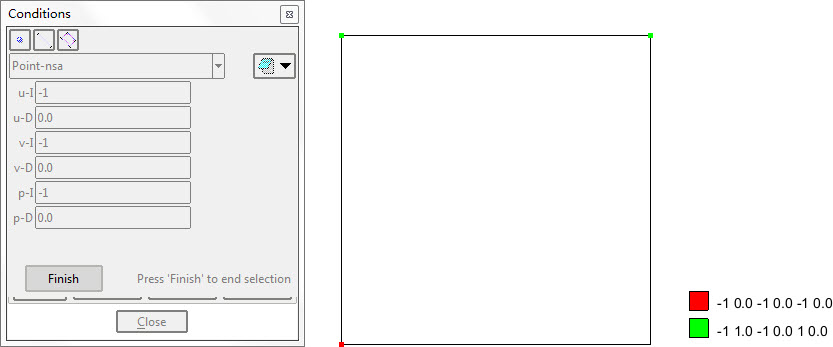
赋初始条件
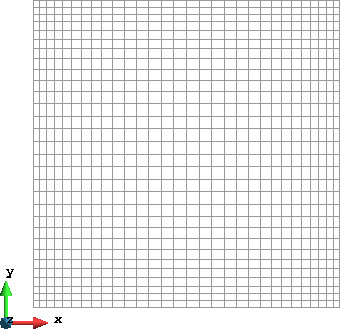
网格剖分
根据所开发程序的计算要求,网格剖分采用 9 节点四边形单元,并对边界位置进行了局部加密。共使用了 900 个单元,3721 个节点。
计算结果
水平流速分量的分布
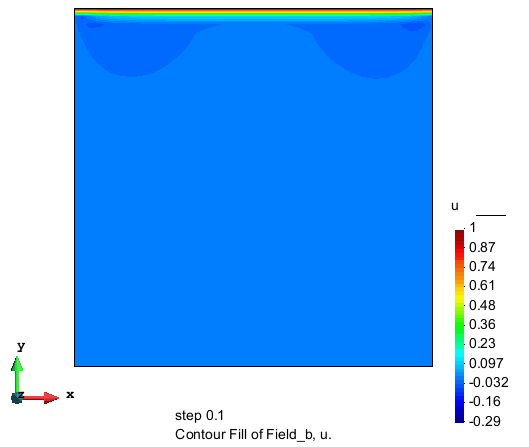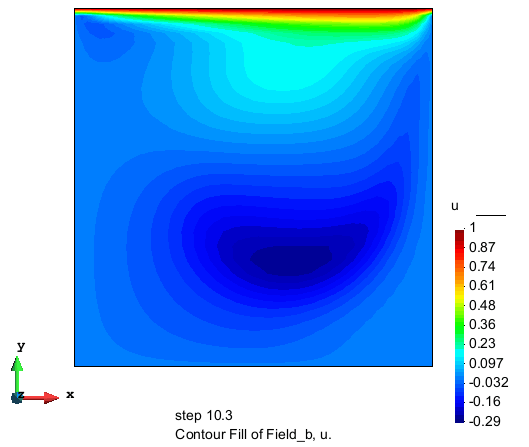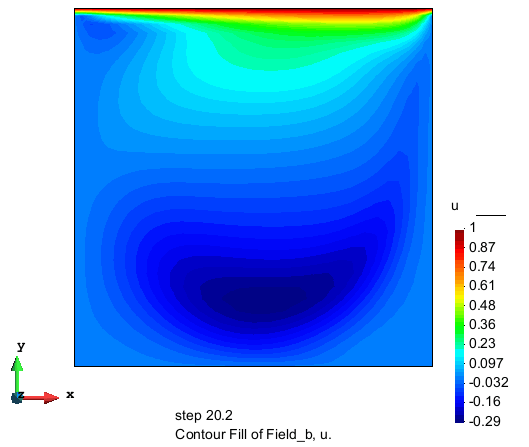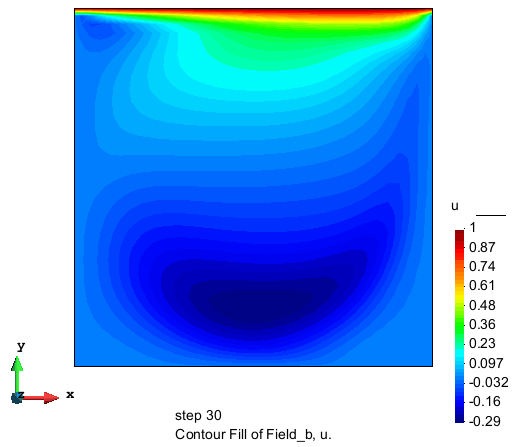
竖直流速分量的分布
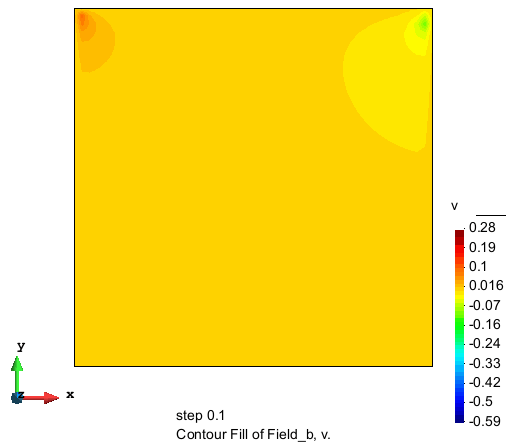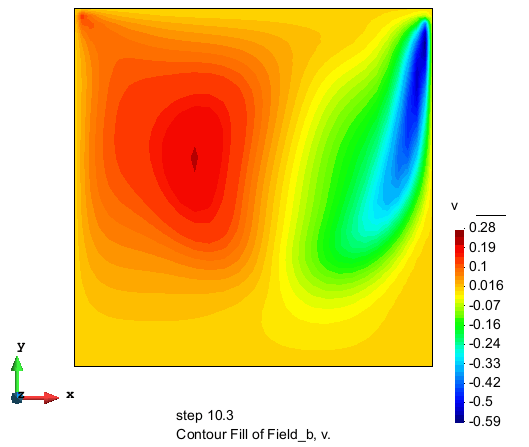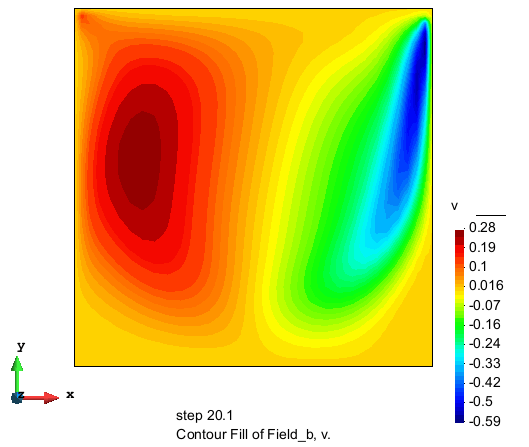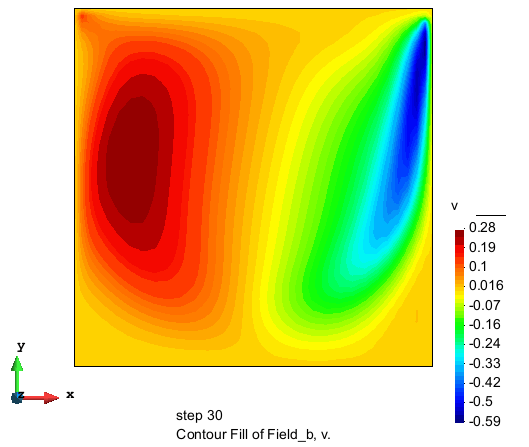
流速大小的分布
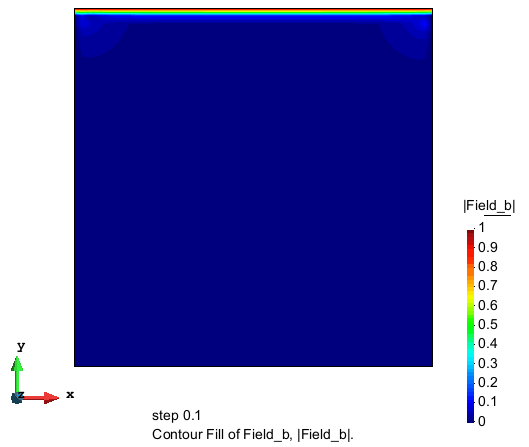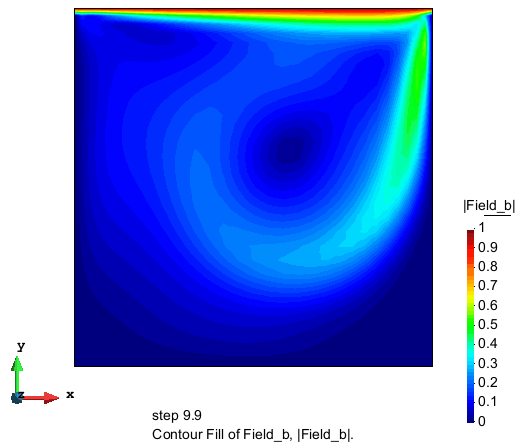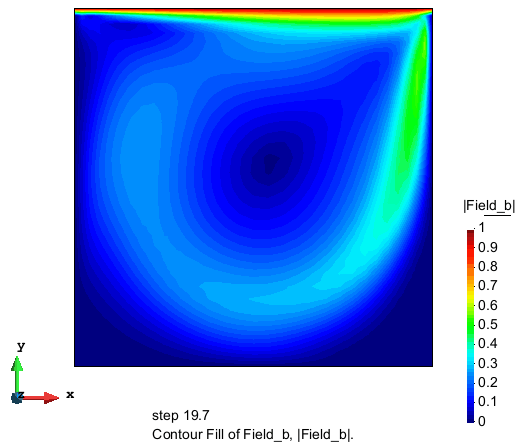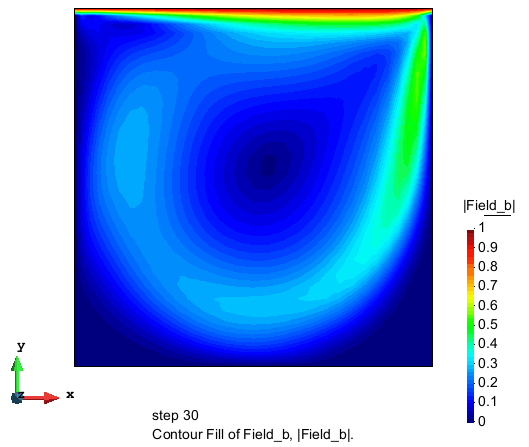
压力的分布
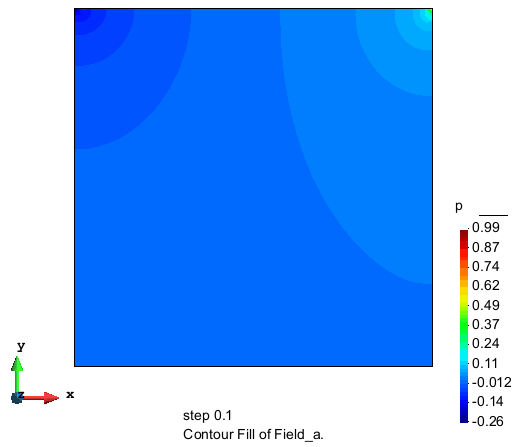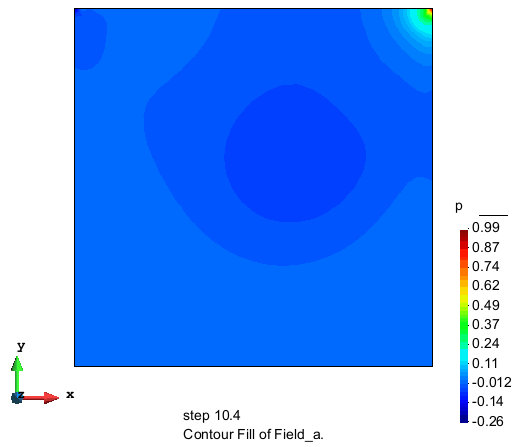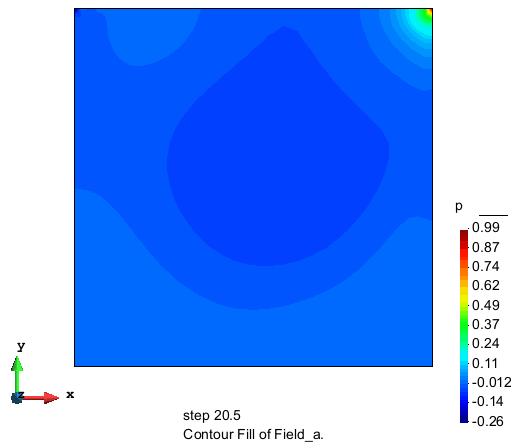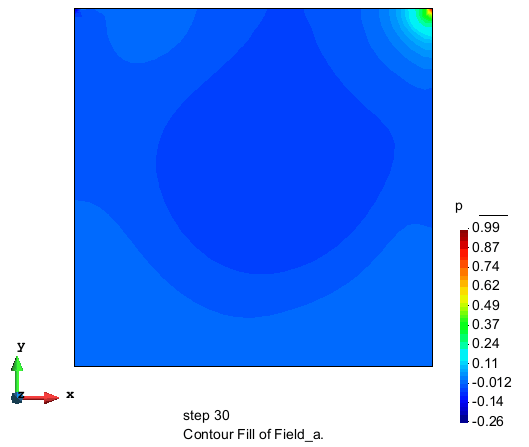
计算结果表明,本节使用的算法在采用较少单元数的情况下也能达到较高的精度和很好的收敛性, 具有很好的应用前景。
小结
本节使用了基于特征线的算子分裂有限元法来求解瞬态 Navier-Stokes 方程。该方法在每一个时间层上, 采用算子分裂法将 Navier-Stokes 方程的对流项与扩散项分开求解。扩散项时间离散采用向后差分格式, 空间离散采用 q9-q4 四边形 Taylo-Hood 单元,隐式求解; 对流项离散采用特征线-Galerkin法, 显式求解。由于通过显示算法避开了非线性迭代过程,所以对时间步长大小有一定的限制。因此,为了实现较高的计算精度,计算时要注意选择合适的时间步长。
参考文献
-
王海娇, 王大国, 熊巨华, 等. 基于特征线的 NS 方程算子分裂有限元法[J]. 中国科学: 技术科学, 2011, 41(8): 1143-1152. ↩





