用点单元实现动态边界条件
关键词: 点单元 动态边界 热传导
本节以二维瞬态热传导问题为例,讲解如何使用点单元实现随时间和空间动态变化的第一类边界条件( Dirichlet 边界条件)。
理论基础
背景介绍
有限元法基本方法本质上就是构造线性方程组 \(Au=f\) 进行求解。其中 $u$ 表示未知数向量,系数矩阵 $A$ 和右端项 $f$ 由单元矩阵组装而成,是已知的。通常矩阵 $A$ 是奇异的,这时需要将第一类边界条件,例如第 $i$ 个分量 $u_i=\bar{u}_i$ ,代入线性方程组,以保证解的唯一性。这种情况下,有 3 种方法可以采用:
- 置大数法
- 划零置一法
- 降阶法
其中划零置一法和降阶法是精确方法,而置大数法则是近似方法。降阶法是 FEtch 系统采用的默认方法,主要用于 $\bar{u}_i$ 为固定值的情况。置大数法则更为灵活,可以通过点单元来轻松实现,更适合用于 $\bar{u}_i$ 动态变化的情况。
置大数法
假设未知数向量 $u$ 的第 $i$ 个分量 $u_i$ 为已知值 $\bar{u}_i$,按照如下方法修改对应的系数矩阵 $A$ 与右端项 $f$ :
- 将 $u_i$ 的对应系数,即主对角元素 $A_{ii}$ ,加上一个极大值 $M$,如 $10^{20}$;
- 将 $u_i$ 的对应右端项分量 $f_i$ ,加上另一个极大值 $\bar{u}_i \times M$ ;
- 其余系数保留不变
这样就得到了一个针对 $u_i$ 的分项方程 \((A_{ii}+10^{20})u_i+小值项= f_i+\bar{u}_i \times 10^{20}\)
从而使得 $u_i\approx\bar{u}_i$ 。
很显然,仅当 $A_{ii}$、 $f_i$ 和 "小值项" 远小于 $10^{20}$ 时,这样的处理才是正确的。
我们发现置大数法在使用的时候只需修改两个对应的系数项即可,简单方便,因此它成为了处理边界条件时经常采用的方法。
下面以二维瞬态热传导问题为例,详细介绍 FEtch 系统是如何通过点单元来使用置大数法的。
控制方程
微分形式
对于二维直角坐标系,瞬态热传导服从如下偏微分方程 \(\rho c \frac{\partial u}{\partial t}-\frac{\partial}{\partial x}\left(k \frac{\partial u}{\partial x}\right)-\frac{\partial}{\partial y}\left(k \frac{\partial u}{\partial y}\right)=0 \ \left(\text{in } \Omega\right) \tag{1}\label{eq1}\) 其中,$\rho$ 表示材料密度,$c$ 为材料的比热,$u$ 表示温度,$k$ 是热传导系数,$x$ 和 $y$ 为二维直角坐标系下的坐标变量,$t$ 为时间。
这里考虑第一类边界条件,它的约束值是时间和空间坐标的函数 \(u=\bar{u}(t,x,y) \ \left(\text{on } \Gamma_1\right)\) 为简单起见,我们取一个三元一次函数 \(\bar{u}(t,x,y)=at+bx+cy \tag{2}\label{eq2}\) 初始条件为 \(u=u_0 \ \left(\text{in } \Omega\right)\)
其中,$u_0$ 为求解域内初始的温度分布。
弱形式
由于仅考虑第一类边界条件,这里的弱形式会简单很多。运用虚位移原理,由微分方程 $\eqref{eq1}$ 两端乘以温度的变分,并在全域上积分,得 \(\int_{\Omega}\left[\rho c \frac{\partial u}{\partial t}-\frac{\partial}{\partial x}\left(k \frac{\partial u}{\partial x}\right)-\frac{\partial}{\partial y}\left(k \frac{\partial u}{\partial y}\right)\right] \delta u d \Omega=0\) 对于二阶导数的部分,利用分部积分将其中的一阶导数转化到温度的变分上,得 \(\int_{\Omega} \rho c \frac{\partial u}{\partial t} \delta u d \Omega+\int_{\Omega}\left(k \frac{\partial u}{\partial x} \frac{\partial \delta u}{\partial x}+k \frac{\partial u}{\partial y} \frac{\partial \delta u}{\partial y}\right) d \Omega=0 \tag{3}\label{eq3}\) 这就是温度场的最终的弱解形式。
离散化
对式 $\eqref{eq3}$ 进行空间离散化后,可进一步写成矩阵形式 \(M \dot{U}+SU=F\) 其中, $U$ 为温度向量,$\dot{U}$ 为温度对时间的导数向量,$M$ 为质量矩阵, $S$ 为刚度矩阵,$F$ 为载荷向量。采用向后差分法进行时域离散,可将上式改写为 \(M \frac{U^{t+\Delta t}-U^{t}}{\Delta t}+S U^{t+\Delta t}=F^{t+\Delta t}\) 整理得 \((M+S \Delta t) U^{t+\Delta t}=F^{t+\Delta t} \Delta t+M U^{t}\) 上标 $t+\Delta t$ 代表当前时间步,$t$ 代表上一时间步。该式即为最终需要求解的线性方程组。
脚本编写
一个具体问题的有限元语言表述,通常需要包含 5 种类型的文件:PDE、FBC、MDI、GCN 和 NFE。下面依次给出详细介绍。
PDE 和 FBC 文件
在这个例子中,只有一个物理场,需要给出温度场对应的 PDE 文件和 FBC 文件。根据有限元语言的语法规则,将方程 $\eqref{eq3}$ 的体积分项写入 PDE 文件如下。
| heat.pde | 说明 |
|---|---|
| defi disp u coor x y shap %1 %2 gaus %3 mass %1 rc mate rho ec ek 5e3; 1e1; 1e2; $c6 rc = rho*ec stif dist = +[u/x;u/x]*ek+[u/y;u/y]*ek load = +[u]*0.0 end |
系统关键字(信息定义) 定义未知量 定义坐标分量 定义采用的形函数 定义采用的积分方式 定义集中质量矩阵,对应式 $\eqref{eq3}$ 左侧第 1 项 定义用到的材料参数和默认参数值 计算热容参数 (空行) 系统关键字(单元刚度矩阵表达式定义) 刚度矩阵项,对应式 $\eqref{eq3}$ 左侧第 2 项 (空行) 荷载向量项 (空行) 系统关键字(文件结束) |
这里将 shap 行和 gaus 行的参数设为待定,参数值 %1、%2 和 %3 将从 MDI 文件中取得。
为了实现动态边界条件,我们继续引入点单元。点单元也叫弹簧单元,是一类特殊的边界单元。点单元的表达式由 FBC 文件给出,具体如下。
| heat.fbc | 说明 |
|---|---|
| defi disp u coor x y mate big pt px py 1e20 1.0 1.0 1.0 stif $c6 ef = pt*time+px*x+py*y dist = +[u;u]*big load = +[u]*big*ef end |
系统关键字(信息定义) 定义未知量 定义坐标分量 定义用到的材料参数和默认参数值 (空行) 系统关键字(单元刚度矩阵表达式定义) 定义动态边界函数,对应式 $\eqref{eq2}$ 刚度矩阵项 (空行) 荷载向量项 (空行) 系统关键字(文件结束) |
以上 mate 语句中定义的材料参数 big 即为置大数法中用到的大数,可根据实际情况调整取值。使用点单元时,首先要通过前处理将其施加在指定的节点上,从而实现定点地修改左端矩阵和右端向量的值。
MDI 文件
MDI 文件负责组织 PDE 和 FBC 文件,声明程序具体使用的坐标系统、单元类型和积分方法。这里文件命名为 lp.mdi,具体内容如下。
| lp.mdi | 说明 |
|---|---|
| 2dxy #a 1 1 u pde heat q4g2 fbc heat s1 # |
在二维直角坐标系下求解 a 场,1 个初值,1 个自由度,自由度名称为 u 调用 heat.pde,采用 4 节点四边形单元,2 点高斯积分 调用 heat.fbc,采用 1 节点的点单元,不需要积分 (文件结束符,可留空) |
GCN 文件
GCN 文件给出计算流程信息,系统规定其文件名字要与 MDI 文件一致。线性抛物方程计算流程比较简单,包含一个时间步的循环过程。只需填写少量代码,对应的 GCN 文件如下。
| lp.gcn | 说明 |
|---|---|
| defi a parb open(1,file='time.dat') read(1,*) dt,tmax close(1) #startsin a time = 0.0 do while (time <= tmax-1d-8) time = time + dt if (time > tmax) then dt = dt-(time-tmax) time = tmax endif #solvsin a enddo |
算法引入段 场 a,采用线性抛物问题的算法 parb.nfe 空一行,开始命令流段 从 time.dat 文件读取时间步参数 初始化 a 场 给 time 赋初始值 循环开始 更新 time 越界修正 求解 a 场 循环结束 |
NFE 文件
GCN 文件使用了 parb 算法,系统会基于模板文件自动生成以下的 lpa.nfe 文件。如果用户有其他需要,可以在此基础上进一步地修改。
| lpa.nfe | 说明 |
|---|---|
| defi stif s mass m load f equation vect u read(s,unod) u matrix = [s]*dt+[m] forc = [f]*dt+[m]*[u] solution u write(s,unod) u gidpost("u",time) u(1) end |
DEFI段 定义刚度矩阵名为 s 定义质量矩阵名为 m 定义载荷向量名为 f (空行) EQUATION段 定义场向量 读入上一时间步的场向量值 方程组左端矩阵 方程组右端向量 (空行) SOLUTION段 定义求解的场向量 临时存储当前的结果,供下一时间步读取 将计算结果写入 GiD 后处理文件 (空行) 结束标记 |
算例1
问题描述
矩形薄板,尺寸为 $1\times0.5\ \mathrm{m}^2$,密度为 $5000\ \mathrm{kg}/\mathrm{m}^3$,比热容为 $20\ \mathrm{J}/\mathrm{kg}/^{\circ}\mathrm{C}$,热传导系数为 $1000\ \mathrm{W}/\mathrm{m}/{ }^{\circ}\mathrm{C}$。初始温度为 $0 { }^{\circ}\mathrm{C}$。取直角坐标系,我们将坐标原点设置在薄板的左下端点。左侧为绝热边界,右侧边界的温度按 $t\ ^{\circ}\mathrm{C/s}$ 动态增长,上下两边绝热。求 $30\ \mathrm{s}$ 内温度场随时间的变化。
前处理
填写材料参数文件
系统自动生成了 lp.mat 文件,用于设置材料参数。参数初始值全部为 PDE 和 FBC 文件给出的默认值。可根据具体问题进行修改。对于本算例,修改完成后的文件内容如下。
| le.mat | 说明 |
|---|---|
| 1 4 aeq4g2 num rho ec ek 1 5e3 20 1e3 # 1 5 als1 num big pt px py 1 1e20 1.0 0 0 # |
4 节点四边形单元 材料参数 参数值 分隔符 点单元 材料参数 参数值 分隔符 |
填写时间步长文件
由 lp.gcn 文件可知,用户自定义了时间步长文件 time.dat,给出时间步长和终止时间。文件内容如下:
- 5 30
由此可知,时间步长为 0.5 s,计算终止时间为 30 s。
赋单元材料
赋初始条件
网格剖分
根据所开发程序的计算要求,采用四边形线性单元进行网格剖分。这里使用了结构化网格,共 231 个节点,200 个单元。

施加第一类边界条件
与之前的加载方式不同,点单元要施加到网格点上,所以在网格剖分之后进行施加。
计算结果
温度场的演化过程

不同时刻温度场的分布
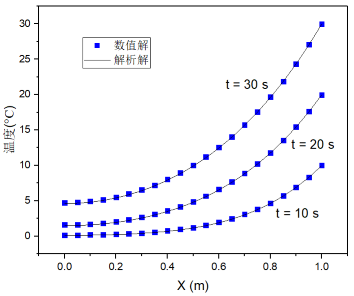
根据数学物理方法中经典的分离变量法,本算例是容易求得解析解的。上图给出了 10 s、20 s、30 s 时的有限元数值解与解析解对比情况,可以发现两者符合得很好,充分证明了算法和程序的有效性。
算例2
问题描述
问题同算例1,此时右侧边界的温度修改为同时是时间和空间坐标的函数,按 $t+10y\ ^{\circ}\mathrm{C}$ 动态增长。求 $30\ \mathrm{s}$ 内温度场随时间的变化。
前处理
同算例1,仅需修改材料参数文件,将 als1 点单元的 py 参数改为 10.0 即可。
计算结果
温度场的演化过程

可以看出,右侧边界的温度随着时间的增长和纵向坐标的不同在不断地发送变化,进一步证明了采用点单元处理动态边界条件的有效性。





